统计学

概率论基础

古典概型

1. 基本公式
   • 排列: 从n个对象中选r个构成一个有序结果
     A_n^r=\frac{n!}{(n-r)!}
   • 组合: 从n个对象中选r个构成一个无序结果
     C_n^r=\frac{n!}{(n-r)!r!}
   • 重复排列: r可辨对象依次放到n个容器的结果数
     U_n^r=n^r
   • 重复组合: r不可辨对象依次放到n个容器的结果数
     H_n^r=C_{n+r-1}^r

常见离散分布

0-1分布

1. 定义
   • \mathrm P\{X=k\}=p^k(1-p)^{1-k}\quad (k=0,1)
2. 矩
   • \mathrm E(X)=p
   • \mathrm D(X)=p(1-p)

二项分布

1. 定义
   • \mathrm P\{X=k\}=\mathrm C_n^k p^k(1-p)^{n-k}\quad (k=0,1,\cdots n)
   • 记为X\sim \mathrm B(n,p)
2. 性质
   • X \sim \mathrm B(n,p)\Leftrightarrow n-X\sim B(n,1-p)
   • 可加性: X \sim \mathrm B(n,p),Y \sim \mathrm B(m,p)，X,Y独立，则X+Y \sim \mathrm B(n+m,p)
   • 最大概率项（用概率比值法）：\begin{cases} \left \lfloor (n+1)p \right \rfloor & \text{ if } (n+1)p\text{不是整数}\\ (n+1)p\text{或}(n+1)p-1 & \text{ if }(n+1)p\text{是整数} \end{cases}
   • 若X\sim \mathrm B(n,p)，当n充分大、p充分小、np适中时，\mathrm B(n,p)\approx \mathrm P(np)
3. 矩
   • \mathrm E(X)=np
   • \mathrm D(X)=np(1-p)

泊松分布

1. 定义
   • \mathrm P\{X=k\}=\frac{\lambda^k}{k!}e^{-\lambda}\quad (k=0,1,\cdots)
   • 记为X\sim \mathrm P(\lambda)
2. 性质
   • 可加性: X \sim \mathrm P(\lambda_1),Y \sim \mathrm P(\lambda_2)，X,Y独立，则X+Y \sim \mathrm P(\lambda_1+\lambda_2)
3. 矩
   • \mathrm E(X)=\lambda
   • \mathrm D(X)=\lambda

超几何分布

1. 定义
   • \mathrm P\{X=k\}=\frac{\mathrm C_{N_1}^k\mathrm C_{N_2}^{n-k}}{\mathrm C_{N_1+N_2}^n}\quad (k=0,1,\cdots,\min(n,N_1))
   • 从N_1个白球和N_2个黑球中一次性拿n个球，抽到k个白球的概率为\mathrm P\{X=k\}
   • 记为X\sim\mathrm h(n,N,M)
2. 性质
   • 当n \ll N_1+N_2, X\sim B\left(n,\frac{N_1}{N_1+N_2}\right)
3. 矩
   • \mathrm E(X)=\frac{nN_1}{N_1+N_2}
   • \mathrm D(X)=\frac{nN_1N_2(N_1+N_2-n)}{(N_1+N_2)^2(N_1+N_2-1)}

几何分布

1. 定义
   • \mathrm P\{X=n\}=p(1-p)^{n-1}\quad (k=0,1,\cdots)
   • 记作X\sim \mathrm{Ge}(p)
2. 性质
   • 无记忆性：\mathrm P\{X=m+n|X\gt m\}=\mathrm P\{X=n\},\ \mathrm P\{X\gt m+n|X\gt m\}=\mathrm P\{X\gt n\}
3. 矩
   • \mathrm E(X)=\frac{1}{p}
   • \mathrm D(X)=\frac{1-p}{p^2}

负二项分布

1. 定义
   • \mathrm P\{X=k\}=\mathrm C_{k-1}^{r-1}p^r(1-p)^{k-r}\quad (k=r,r+1,\cdots)
   • 表示使得事件发生r次所需的实验次数k的分布
   • 记作X\sim\mathrm{Nb}(r,p)
2. 性质
   • \mathrm{Nb}(1,p)=\mathrm{Ge}(p)
   • 可加性: \mathrm{Nb}(r_1,p)+\mathrm{Nb}(r_2,p)=\mathrm{Nb}(r_1+r_2,p)

常见连续分布

均匀分布

1. 定义
   {f(x)}=\left\{\begin{array}{ll}\frac{1}{b-a} & a\lt x\lt b \\0 & \text {其他}\end{array}\right.\quad {F(x)}=\left\{\begin{array}{ll}0 & x\lt a \\ \frac{x-a}{b-a} & a \leqslant x\lt b \\1 & x \geqslant b \end{array}\right.
   • 记为X \sim \mathrm U(a, b)
2. 矩
   • \mathrm E(X)=\frac{a+b}{2}
   • \mathrm D(X)=\frac{(b-a)^2}{12}

指数分布

1. 定义
   {f(x)}=\left\{\begin{array}{ll}\lambda \mathrm{e}^{-\lambda x} & x>0 \\0 & x \leqslant0\end{array}\right.\quad {F(x)}=\left\{\begin{array}{ll}1-\mathrm{e}^{-\lambda x} & x>0 \\0 & x \leqslant0\end{array}\right.
   • 记为X \sim \mathrm{Exp}(\lambda)
2. 性质
   • \mathrm{P}\{X\gt x\}=\mathrm{e}^{-\lambda x}
   • 无记忆性：\mathrm{P}\{X\gt s+t|X\gt s\}=\mathrm{P}\{X\gt t\}
   • 若事件在t时间内发生次数服从\mathrm P(\lambda t)，则两次发生间隔时间服从\mathrm{Exp}(\lambda)
3. 矩
   • \mathrm E(X)=\frac{1}{\lambda}
   • \mathrm D(X)=\frac{1}{\lambda^2}

正态分布

1. 定义
   {f(x)}=\frac{1}{\sqrt{2\pi} \sigma} \mathrm{e}^{-\frac{(x-\mu)^2}{2\sigma^2}}\quad{F(x)}=\frac{1}{\sqrt{2\pi} \sigma} \int_{-\infty}^x \mathrm{e}^{-\frac{(t-\mu)^2}{2\sigma^2}} \mathrm{~d} t
   • 记为X \sim \mathrm N(\mu,\sigma^2)
   • 定义\Phi\left(\frac{x-\mu}{\sigma}\right) = {F(x)}=\mathrm{P}\{X \leqslant x\}，\Phi(x)为标准正态分布的分布函数
   • 定义\frac{1}{\sigma}\phi\left(\frac{x-\mu}{\sigma}\right) ={F^\prime(x)}= {f(x)}，\phi(x)为标准正态分布的概率密度（[\Phi(g(x))]^\prime=g(x)^\prime\phi(g(x))）
2. 性质
   • 最大值f(\mu)=\frac{1}{\sqrt{2\pi}\sigma}，驻点\mu，拐点\mu+\sigma
   • \mathrm N(\mu_X,\sigma_X^2)\pm\mathrm N(\mu_Y,\sigma_Y^2)=\mathrm N(\mu_X\pm\mu_Y,\sigma_X^2+\sigma_Y^2)，前提是独立
   • a+b\mathrm N(\mu,\sigma^2)=\mathrm N(a+b\mu,b^2\sigma^2)（多元正态分布也一样）
   • \Phi(-x)=1-\Phi(x),\phi(-x)=\phi(x)
   • \int_{0}^{+\infty}x^2\phi(x)dx=\frac{1}{2},\int_{0}^{+\infty}x\phi(x)dx=\frac{1}{\sqrt{2\pi}},\int_{0}^{+\infty}\phi(x)dx=\frac{1}{2}
3. 矩
   • \mathrm E(X)=\mu
   • \mathrm D(X)=\sigma^2
   • \nu_k=\mathrm E\left[X-\mathrm E(X)\right]^k=\begin{cases} (k-1)!!\sigma^k & \text{ if }\ \text{k为偶数} \\ 0 & \text{ if }\ \text{k为奇数} \end{cases}
   • \mu_k=\mathrm E\left(X^k\right)=\mathrm E\left[X-\mathrm E(X)+\mathrm E(X)\right]^k，利用\nu_k的展开式递推

伽马分布

1. 定义
   f(x)= \begin{cases}\frac{\lambda^\alpha}{\Gamma(\alpha)} x^{\alpha-1} \mathrm{e}^{-\lambda x}, & x \ge 0\\0, & x\lt0\end{cases}
   • 记为X\sim\mathrm{Ga}(\alpha,\lambda)
2. 性质
   • \mathrm{Ga}(1,\lambda)=\mathrm{Exp}(\lambda)
   • \mathrm{Ga}\left(\frac{n}{2},\frac{1}{2}\right)=\chi^2(n)
   • 可加性: \mathrm{Ga}(\alpha_1,\lambda)+\mathrm{Ga}(\alpha_2,\lambda)=\mathrm{Ga}(\alpha_1+\alpha_2,\lambda)
   • 伸缩性: \mathrm{Ga}(\alpha,\lambda)=k\mathrm{Ga}(\alpha,k\lambda)
   • 若事件在t时间内发生次数服从\mathrm P(\lambda t)，则第n次发生的时间服从\mathrm{Ga}(n,\lambda)
3. 矩
   • \mathrm E(X)=\frac{\alpha}{\lambda}
   • \mathrm D(X)=\frac{\alpha}{\lambda^2}

贝塔分布

1. 定义
   f(x)= \begin{cases}\frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)} x^{a-1}(1-x)^{b-1}, &0\le x\le 1, \\0, & \text {其他, }\end{cases}
2. 矩
   • \mathrm E(X)=\frac{a(a+1)}{(a+b)(a+b+1)}
   • \mathrm D(X)=\frac{ab}{(a+b)^2(a+b+1)}

卡方分布

1. 定义
   • X_1,\cdots,X_n独立且均服从标准正态分布\mathcal{N}，则
     \chi^2(n)=\sum X_i^2
     为自由度为n的卡方分布
   • 若\mathrm P\{\chi^2(n)\gt\chi^2_\alpha(n)\}=\alpha，记\chi^2_\alpha(n)为\chi^2(n)的上\alpha位分位点
2. 性质
   • \mathcal{N}^2\sim\chi^2(1)
   • 可加性: \chi^2(n_1)+\chi^2(n_2)=\chi^2(n_1+n_2)
3. 矩
   • \mathrm E\left[\chi^2(n)\right]=n
   • \mathrm D\left[\chi^2(n)\right]=2n

t分布

1. 定义
   • 若\mathcal N,\chi^2(n)独立，则
     \tau(n)=\frac{\mathcal N}{\sqrt{\chi^2(n)/n}}
   • 若\mathrm P\{\tau(n)\gt\tau_\alpha(n)\}=\alpha，记\tau_\alpha(n)为\tau的上\alpha位分位点
2. 性质
   • \tau_{1-\alpha}(n)=-\tau_\alpha(n)
   • \tau(n)\xrightarrow[n]{L} \mathcal N
   • \tau^2(n)\sim \mathcal F(1,n)
3. 矩
   • \mathrm E\left[\tau(n)\right]=0
   • \mathrm D\left[\tau(n)\right]=\frac{n}{n-2}

F分布

1. 定义
   • 若\chi^2(m),\chi^2(n)独立，则
     \mathcal F(m,n)=\frac{\chi^2(m)/m}{\chi^2(n)/n}
   • 若\mathrm P\{\mathcal F(m,n)\gt\mathcal F_\alpha(m,n)\}=\alpha，记\mathcal F_\alpha(m,n)为\mathcal F(m,n)的上\alpha位分位点
2. 性质
   • \frac{1}{\mathcal F(m,n)}\sim\mathcal F(n,m)
   • \mathcal F_{1-\alpha}(m,n)=\frac{1}{\mathcal F_{\alpha}(n,m)}
3. 矩
   • \mathrm E\left[\mathcal F(m,n)\right]=\frac{n}{n-2}
   • \mathrm D\left[\mathcal F(m,n)\right]=\frac{2n^2(m+n-2)}{m(n-2)^2(n-4)}

其它

1. 常用公式
   \begin{align} &r\begin{pmatrix}n\\r\end{pmatrix}=n\begin{pmatrix}n-1\\r-1\end{pmatrix} \\\\ &\int_0^{+\infty} x^{\alpha}e^{-x}\mathrm d x=\Gamma(\alpha + 1)=\alpha ! \\ &\int_0^{1} x^{a}(1-x)^b\mathrm d x=\frac{\Gamma(a+1)\Gamma(b+1)}{\Gamma(a+b+2)} \\ &\left(\frac{1}{2}\right)!=\frac{\sqrt\pi}{2},\left(-\frac{1}{2}\right)!=\sqrt\pi \\\\ &\int_{-\infty}^{+\infty} e^{-x^2}\mathrm d x=\sqrt{\pi} \end{align}
2. 联合分布的转换
   p_{X,Y}(x,y)=p_{F(X,Y),G(X,Y)}(F(x,y),G(x,y))\begin{vmatrix} \frac{\partial F}{\partial x} & \frac{\partial F}{\partial y} \\ \frac{\partial G}{\partial x} & \frac{\partial G}{\partial y} \end{vmatrix}
   • 要使得F,G能够覆盖全部定义域，否则要考虑多解并将每个表达式加起来p_{X,Y}(x,y)=\sum p_{F_i(X,Y),G_i(X,Y)}(F_i(x,y),G_i(x,y))
3. 条件期望
   E(X\mid Y=y)=\begin{cases}\sum x_i P(X=x_i \mid Y=y) \\ \int_{D^\prime} x \frac{p_{X,Y}(x,y)}{p_Y(y)} \mathrm d x\end{cases}
   • 计算条件概率利用期望公式求解，或将条件代入X的分布得到新分布，对x进行积分
   • 条件期望的结果一定是关于y的函数，并且有E(X\mid Y=y)=g(y)\Rightarrow E(X\mid Y)=g(Y)
4. 重期望公式
   E(Y)=\sum E(Y|X=x)P(X=x)=\int E(Y|X=x)f(x)\mathrm dx=E[E(Y|X)]
   • 当分布Y的参数来源于另一个分布X时，利用此公式求期望方差等
   • 先计算E(Y|X=x)=g(x)，于是E(Y)=E[E(Y|X)]=E[g(X)]
5. n项分布
   P(X_1=n_1,X_2=n_2,\cdots,X_k=n_k)=\frac{(\sum n_i)!}{\prod n_i}\prod p_i^{n_i}
6. n个元素圆排列种数: (n-1)!
7. 可分离变量且矩形区域则一定独立，不是矩形一定不独立

大数定律

收敛性

依概率收敛

1. 定义
   • 设\left\{X_n\right\}为一随机变量序列，X为一随机变量
   • 若对任意\varepsilon\gt 0，有P\left(\left|X_n-X\right| \ge \varepsilon\right) \rightarrow0\quad(n \rightarrow \infty)
   • 则称序列\left\{X_n\right\}依概率收敛于X ，记作X_n \xrightarrow{P} X
2. 性质
   • 若X_n \xrightarrow{P} a,\ Y_n \xrightarrow{P} b，则
     X_n \pm Y_n \xrightarrow{P} a \pm b
     X_n \times Y_n \xrightarrow{P} a \times b
     X_n \div Y_n \xrightarrow{P} a \div b\quad (b \neq0)

依分布收敛

1. 定义
   • 设\left\{X_n\right\}为一随机变量序列，\left\{F_n(x)\right\}为其分布函数序列，X为一随机变量，F(x)为其分布函数
   • 若对于F(x)的任意连续点，都有\lim_{n \rightarrow \infty} F_n(x)={F(x)}
   • 则称\left\{F_n(x)\right\}弱收敛于F(x)，\left\{X_n\right\}依分布收敛于X，记作F_n(x) \xrightarrow{W} {F(x)}，X_n \xrightarrow{L} X
2. 性质
   • X_n \xrightarrow{P} X \Longrightarrow X_n \xrightarrow{L} X
   • X_n \xrightarrow{P} c \Longleftrightarrow X_n \xrightarrow{L} c

特征函数

1. 定义
   • X为一随机变量，则其特征函数为
     \varphi(t)=E\left(\mathrm{e}^{\mathrm{i}t X}\right)\quad(-\infty\lt t\lt \infty)
   • 对于连续随机变量X
     \varphi(t)=\int_{-\infty}^{\infty} \mathrm{e}^{\mathrm{i} t x} p(x) \mathrm{d} x\quad(-\infty\lt t\lt \infty)
   • 对于离散随机变量X
     \varphi(t)=\sum_{k=1}^{\infty} \mathrm{e}^{\mathrm{i}tx_k} p_k\quad(-\infty\lt t\lt \infty)
2. 常用分布的特征函数
   • 单点分布P(X=a)=1
     \varphi(t)=e^{\mathrm{i}ta}
   • 0-1分布B(1,p)
     \varphi(t)=pe^{\mathrm{i}t}+1-p
   • 二项分布B(n,p)
     \varphi(t)=\left(pe^{\mathrm{i}t}+1-p\right)^n
   • 泊松分布P(\lambda)
     \varphi(t)=e^{\lambda(e^{\mathrm{i}t}-1)}
   • 几何分布Ge(p)
     \varphi(t)=\frac{pe^{\mathrm it}}{1-(1-p)e^{\mathrm it}}
   • 负二项分布Nb(r,p)
     \varphi(t)=\left[\frac{pe^{\mathrm it}}{1-(1-p)e^{\mathrm it}}\right]^r
   • 均匀分布U(a,b)
     \varphi(t)=\frac{\mathrm{e}^{\mathrm{i} b t}-\mathrm{e}^{\mathrm{i} a t}}{\mathrm{i}t(b-a)}
   • 标准正态分布N(0,1)
     \varphi(t)=e^{-\frac{t^2}{2}}
   • 正态分布N(\mu,\sigma^2)
     \varphi(t)=e^{\mathrm{i}\mu t-\frac{\sigma^2t^2}{2}}
   • 伽马分布Ga(\alpha,\lambda)
     \varphi(t)=\left(1-\frac{\mathrm{i} t}{\lambda}\right)^{-\alpha}
   • 指数分布Exp(\lambda)
     \varphi(t)=\left(1-\frac{\mathrm{i} t}{\lambda}\right)^{-1}
   • 卡方分布\chi^2(n)
     \varphi(t)=(1-2\mathrm{i} t)^{-n /2}
   • 柯西分布Cau(0,1)
     e^{|\mathrm it|}
3. 性质
   • |\varphi(t)| \leqslant \varphi(0)=1
   • \varphi(t)与\varphi(-t)共轭
   • \varphi_{aX+b}(t)=\mathrm{e}^{\mathrm{i} b t} \varphi_X(a t)
   • \varphi_{X+Y}(t)=\varphi_{X}(t)\varphi_{Y}(t)
   • \varphi^{(k)}(0)=\mathrm{i}^k E\left(X^k\right)
   • E(X)=\frac{\varphi^{\prime}(0)}{\mathrm{i}},\ \operatorname{Var}(X)=-\varphi^{\prime \prime}(0)+\left(\varphi^{\prime}(0)\right)^2
4. 唯一性定理：分布函数由特征函数唯一决定
   • 逆转公式
     F\left(x_2\right)-F\left(x_1\right)=\lim_{T \rightarrow \infty} \frac{1}{2\pi} \int_{-T}^T \frac{\mathrm{e}^{-\mathrm{i}tx_1}-\mathrm{e}^{-\mathrm{i} t x_2}}{\mathrm{i} t} \varphi(t) \mathrm{d} t
   • 若X为连续型随机变量，且\int_{-\infty}^{\infty}|\varphi(t)| \mathrm{d} t\lt\infty，则
     p(x)=\frac{1}{2\pi} \int_{-\infty}^{\infty} \mathrm{e}^{-\mathrm{i} t x} \varphi(t) \mathrm{d} t
5. 连续性定理：特征函数与弱收敛等价
   F_n(x) \xrightarrow{W} {F(x)}\Longleftrightarrow \varphi_n(x) \rightarrow {\varphi(x)}

大数定律

1. 大数定律
   • 切比雪夫不等式
     P\left\{|X-E(X)|\gt \varepsilon \right\}\lt\frac{Var(X)}{\varepsilon^2}
   • 对任意\varepsilon\gt 0
     \lim_{n \rightarrow+\infty} P\left\{\left|\frac{1}{n} \sum_{i=1}^n X_i-\frac{1}{n} \sum_{i=1}^n E\left(X_i\right)\right| \lt \varepsilon\right\}=1
2. 伯努利大数定律
   • 记S_n为n次伯努利实验中事件A发生次数（即S_n\sim B(n,p)）
   • 此时有\frac{1}{n}S_n \xrightarrow{P} p
3. 切比雪夫大数定律
   • 设\{X_n\}为两两不相关的随机变量序列，X_i方差存在且有共同上界
   • 此时有\frac{1}{n}\sum_{i=1}^nX_i \xrightarrow{P} \frac{1}{n}\sum_{i=1}^n E(X_i)
4. 马尔科夫大数定律
   • 设\{X_n\}为随机变量序列，满足\frac{1}{n^2} \operatorname{Var}\left(\sum_{i=1}^n X_i\right) \rightarrow0
   • 此时有\frac{1}{n}\sum_{i=1}^nX_i \xrightarrow{P} \frac{1}{n}\sum_{i=1}^n E(X_i)
5. 辛钦大数定律
   • 设\{X_n\}为独立同分布的随机变量序列，X_i期望存在（设为a）
   • 此时有\frac{1}{n}\sum_{i=1}^nX_i \xrightarrow{P} a

中心极限定理

独立同分布

1. 列维-林德伯格中心极限定理
   • 设\{X_n\}为独立同分布的随机变量序列，且E\left(X_i\right)=\mu,\ Var\left(X_i\right)=\sigma^2\gt 0，则
     \sum_{i=1}^n X_i \xrightarrow{L} N(n\mu,n\sigma^2)
2. 棣莫弗-拉普拉斯中心极限定理
   • 记S_n为n次伯努利实验中事件A发生次数（即S_n\sim B(n,p)），则
     S_n \xrightarrow{L} N(np,np(1-p))
   • 由于S_n为离散随机变量，往往采用修正的正态分布近似
     \begin{align} & P(a\le S_n\le b)\approx P(a{\color{Red} -0.5}\lt S_n\lt b{\color{Red} +0.5})= \Phi\left(\frac{b-np{\color{Red} +0.5} }{\sqrt{np(1-p)}}\right)-\Phi\left(\frac{a-np{\color{Red}- 0.5}}{\sqrt{np(1-p)}}\right) \\ & P(S_n=k)=P(k\le S_n\le k)\approx \frac{1}{\sqrt{np(1-p)}}\varphi\left(\frac{b-np}{\sqrt{np(1-p)}}\right) \end{align}

独立不同分布

1. 林德伯格中心极限定理
   • 设\{X_n\}为独立的随机变量序列，E(X_i)=\mu_i,\ Var(X_i)=\sigma_i^2，且满足林德伯格条件(略),则
     \frac{1}{B_n}\sum_{i=1}^{n}\left(X_i-\mu_i\right) \xrightarrow{L} N(0,1)
     其中B_n=\sqrt{\sum_{i=1}^{n}\sigma_i^2}
2. 李雅普诺夫中心极限定理
   • 设\{X_n\}为独立的随机变量序列，E(X_i)=\mu_i,\ Var(X_i)=\sigma_i^2，且满足
     \exists \delta\gt0\ \mathrm{s.t.}\ \lim_{n \rightarrow \infty} \frac{1}{B_n^{2+\delta}} \sum_{i=1}^n E\left(\left|X_i-\mu_i\right|^{2+\delta}\right)=0
     则上述中心极限定理也成立

统计量

定义

1. 概念
   • 统计量：关于样本的函数T=T(x_1,\cdots,x_n)，不包含其它未知量
   • 抽样分布：统计量的T的分布，其分布往往依赖其它未知量
   • 形如(T_1,T_2)=(X_{(1)},X_{(2)})也是统计量
2. 原点矩与中心矩
   a_k=\frac{1}{n} \sum_{i=1}^n x_i^k\quad b_k=\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar x\right)^k
3. 样本均值
   \bar{x}=\frac{1}{n}\sum_{i=1}^nx_i
   • E(\bar{x})=\mu，Var(\bar{x})=\frac{\sigma^2}{n}
4. 样本方差
   s^2=\frac{1}{n-1} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2
   • E(s^2)=\sigma^2，Var(s^2)=\frac{\sigma^4}{n}\left(\frac{b_4}{\sigma^4}-\frac{n-3}{n-1}\right)
   • 样本均值与样本方差相互独立
5. 样本协方差
   s_w^2=\frac{(m-1) s_x^2+(n-1) s_y^2}{m+n-2}
6. 样本偏度
   \hat{\beta}_s=\sqrt{\frac{b_3^2}{b_2^{3}}}
   • 偏度大于0则右偏，小于0则左偏
7. 样本峰度
   \hat{\beta}_k={\frac{b_4}{b_2^{2}}}-3
   • 峰度大于0则尖峰细尾，小于0则平坦肥尾
8. 第i次序统计量
   x_{(i)}
   • 将样本x_1,\cdots,x_n从小到大排序后第i个值
   • x_{(1)}又叫最小次序统计量，x_{(n)}又叫最大次序统计量
   • 各次序统计量之间既不独立，分布也不相同
9. 样本分位数与中位数
   \begin{align} &m_{p}= \begin{cases} x_{\left(\left[np+1\right]\right)} & np+1 \text {不为整数 } \\ \frac{1}{2}\left(x_{\left(np\right)}+x_{\left(np+1\right)}\right) & np \text {为整数 } \end{cases} \\\\ &m_{0.5}= \begin{cases} x_{\left(\frac{n+1}{2}\right)} & n \text {为奇数 } \\ \frac{1}{2}\left(x_{\left(\frac{n}{2}\right)}+x_{\left(\frac{n}{2}+1\right)}\right) & n \text {为偶数 } \end{cases} \end{align}
   • 连续随机变量下，满足p=F(x_p)

分布

1. 样本均值
   • 若总体分布为N(\mu,\sigma^2)，则
     \bar{x}\sim N\left(\mu,\frac{\sigma^2}{n}\right)
   • 若总体期望为\mu，样本方差为s^2，则
     \bar{x}\sim \mu+\frac{s}{\sqrt n}t(n-1) \dot{\sim} N\left(\mu,\frac{s^2}{n}\right)
   • \sigma_x^2,\sigma_y^2已知时，则
     \bar{x}-\bar{y} \sim N \left( \mu_x-\mu_y , \frac{\sigma_x^2}{m}+\frac{\sigma_y^2}{n}\right)
   • \sigma_x^2,\sigma_y^2相等但未知时，则
     \bar{x}-\bar{y} \sim \mu_x-\mu_y + \sqrt{\frac{m+n}{m n}} s_w t(m+n-2)
   • \sigma_x^2/\sigma_y^2=c时，则
     \bar{x}-\bar{y} \sim \mu_x-\mu_y + \sqrt{\frac{cm+n}{m n}} s_w t(m+n-2)
   • m,n都很大时，则
     \bar{x}-\bar{y} \dot{\sim} N \left( \mu_x-\mu_y , \frac{s_x^2}{m}+\frac{s_y^2}{n}\right)
   • 一般情况下
     \begin{align} &\bar{x}-\bar{y}\sim \mu_x-\mu_y+ s_0t(l) \\\\ \text{其中}\quad &s_0=\sqrt{\frac{s_x^2}{m}+\frac{s_y^2}{n}}\quad\quad l=\frac{s_0^4}{\frac{s_x^4}{m^2(m-1)}+\frac{s_y^4}{n^2(n-1)}} \end{align}
   • 指数分布Exp(1/\theta)
     \bar x\sim \frac{\theta}{2n}\chi^2(2n)
2. 样本方差
   • 若总体分布为N(\mu,\sigma^2)，则
     s^2 \sim \frac{\sigma^2}{n-1}\chi^2(n-1)
   • 若x_1,\cdots,x_m来自分布N(\mu_x,\sigma^2_x)，y_1,\cdots,y_n来自分布N(\mu_y,\sigma^2_y)，则
     \frac{s_x^2}{s_y^2} \sim \frac{\sigma_x^2}{\sigma_y^2} {F(m-1, n-1)}
3. 样本协方差
   • 若\sigma_x^2=\sigma_y^2=\sigma^2
     s_w=\frac{\sigma^2}{m+n-2}\chi^2(m+n-2)
4. 单个次序统计量
   • x_{(k)}的密度函数
     p_k(x)=n!\cdot\frac{F^{k-1}(x)}{(k-1)!}\cdot p(x)\cdot\frac{[1-F(x)]^{n-k}}{(n-k)!}
   • x_{(1)},x_{(n)}的密度函数
     \begin{align} &p_1(x)=n({F(x)})^{n-1} p(x) \\ &p_k(x)=n(1-{F(x)})^{n-1} p(x) \end{align}
5. 多个次序统计量
   • \left(x_{(i)},x_{(j)}\right)\quad (i\lt j)的联合分布密度函数
     p_{i j}(y, z)=n!\cdot\frac{F^{i-1}(y)}{(i-1)!}\cdot p(y)\cdot\frac{[F(z)-F(y)]^{j-i-1}}{(j-i-1)!}\cdot p(z)\cdot\frac{[1-F(z)]^{n-j}}{(n-j)!} \quad y \leqslant z
6. 分位数
   \begin{align} &m_p \dot{\sim} N\left(x_p, \frac{p(1-p)}{n \cdot p^2\left(x_p\right)}\right) \\\\ &m_{0.5} \dot{\sim} N\left(x_{0.5}, \frac{1}{4n \cdot p^2\left(x_{0.5}\right)}\right) \end{align}

充分性

1. 定义
   • 当给定统计量T=T(x_1,\cdots,x_n)的值后，若样本的x_1,\cdots,x_n的条件分布与总体分布函数F(x;\theta)的参数\theta无关，则T是充分统计量
2. 因子分解定理
   • 统计量T=T(x_1,\cdots,x_n)为充分统计量的充分必要条件是，总体概率函数f(x;\theta)可以分解为g(T,\theta)h(x_1,\cdots,x_n)的形式

参数估计

点估计

1. 定义
   • 设x_1,\cdots,x_n是来自总体的样本，则\hat\theta=\hat\theta(x_1,\cdots,x_n)为\theta的点估计量
2. 无偏性
   • 若E(\hat\theta)=\theta，则\hat\theta是\theta的无偏估计
   • 若E(\hat\theta)\rightarrow\theta，则\hat\theta是\theta的渐进无偏估计
   • 即使\hat\theta是\theta的无偏估计，g(\hat\theta)一般不是g(\theta)的无偏估计
   • 有时参数可能不存在无偏估计，此时称参数不可估
3. 刀切法
   • 设T(\boldsymbol x)是g(\theta)的估计量，且满足
     E(T(\boldsymbol x))=g(\theta)+\circ\left(\frac{1}{n}\right)
   • 则统计量T_j(\boldsymbol x)=n T(\boldsymbol{x})-\frac{n-1}{n} \sum_{i=1}^n T\left(\boldsymbol{x}_{(-i)}\right)一定是渐进性更好的统计量，满足
     E(T_j(\boldsymbol x))=g(\theta)+\circ\left(\frac{1}{n^2}\right)
4. 有效性
   • 对于两个无偏估计\hat\theta_1和\hat\theta_2，若{Var}\left(\hat{\theta}_1\right) \leqslant {Var}\left(\hat{\theta}_2\right)，则\hat\theta_1比\hat\theta_2有效

矩估计

1. 定义
   • 用样本均值估计总体均值
   • 用样本方差估计总体方差
   • 用事件出现频率估计事件发生概率
   • 用样本分位数估计总体分位数
2. 相合性
   • 若\hat\theta_n \xrightarrow{P} \theta则称\hat\theta_n为\theta的相合估计
   • 若E(\hat\theta_n)\rightarrow \theta,Var(\hat\theta_n)\rightarrow 0，则\hat\theta_n是\theta的相合估计
   • 若\hat{\boldsymbol\theta_n}是\boldsymbol\theta的相合估计，则g(\hat{\boldsymbol\theta_n})是g(\boldsymbol\theta)的相合估计

MLE

1. 定义
   • 令似然函数最大时的统计量作为估计量
   • 若\hat{\theta}是\theta最大似然估计，则g(\hat\theta)是g(\theta)最大似然估计
   • 根据\hat{\theta}置信区间得到g(\hat\theta)的置信区间，注意单尾时二者方向可能会不同
2. 渐进正态性
   • 若估计量\hat{\theta_n}满足
     \frac{\hat{\theta}_n-\theta}{\sigma_n(\theta)} \xrightarrow{L} N(0,1)
   • 则\hat{\theta_n}服从渐进正态分布，记为\hat{\theta}_n\sim AN(\theta,\sigma_n^2(\theta))，\sigma_n^2(\theta)称为渐进方差
3. 最大似然估计通常满足渐进正态性
   \hat{\theta}_n\sim AN(\theta,\frac{1}{nI(\theta)})
   • 其中I(\theta)称为费希尔信息量
     I(\theta)=E\left[\frac{\partial}{\partial \theta} \ln p(x ; \theta)\right]^2=-E\left[\frac{\partial^2}{\partial \theta^2} \ln p(x ; \theta)\right]
   • 参数变换后的费希尔信息量
     I(g(\theta))=\frac{I(\theta)}{[g^\prime(\theta)]^2}

UMVUE

1. 一致最小均方误差估计
   • 均方误差
     {MSE}(\hat{\theta})=E(\hat{\theta}-\theta)^2={Var}(\hat{\theta})+(E(\hat{\theta})-\theta)^2
   • 对于一个估计类，使得均方误差最小的那个估计
2. 一致最小方差无偏估计UMVUE
   • 当估计为无偏估计，均方误差退化为方差，一致最小均方误差估计退化为一致最小方差无偏估计
   • 在一个无偏估计类中，使得方差最小的那个估计为UMVUE
   • UMVUE的条件：估计量为无偏估计，且与任意期望为零的估计量不相关
   • UMVUE构造方法：先确定充分统计量，求期望得到估计量表达式，再证明与任意0期望估计量不相关
3. 充分性原则
   • 无偏估计\hat\theta对充分统计量T求条件期望，可以构造出方差不更大的无偏估计\tilde{\theta}=E(\hat{\theta} \mid T)
4. 克拉默-拉奥不等式
   • 设T=T(\boldsymbol x)是g(\theta)的无偏估计，则
     Var(T)\ge \frac{\left[g^\prime(\theta)\right]^2}{nI(\theta)}
   • 该下限称为g(\theta)的C-R下界，达到下界的无偏估计为有效估计，此时也一定是UMVUE

贝叶斯估计

1. 概念
   • 假设已知要估计的参数的某些特征（称为先验信息），在原参数估计的基础上融入先验信息得到参数的后验分布
   • 后验分布的期望就是贝叶斯估计
2. 步骤
   • 根据先验信息得到要估计的参数的概率分布\pi(\theta)
   • 已知总体的分布，得到总体条件分布p(x\mid\theta)
   • 样本的联合条件分布p(x_1,\cdots,x_n\mid\theta)=p(x_1\mid\theta)\cdots p(x_n\mid\theta)
   • 样本的联合分布为h(x_1,\cdots,x_n,\theta)=p(x_1\mid\theta)\cdots p(x_n\mid\theta)\pi(\theta)
   • 样本边际分布为m(x_1,\cdots,x_n)=\int_{\theta \in \Theta}p(x_1\mid\theta)\cdots p(x_n\mid\theta)\pi(\theta)\mathrm d\theta
   • 参数的后验分布为\pi(\theta|x_1,\cdots,x_n)=\frac{h(x_1,\cdots,x_n,\theta)}{m(x_1,\cdots,x_n)}
   • 于是贝叶斯估计为\hat\theta=E(\pi(\theta|x_1,\cdots,x_n))
3. 共轭先验分布
   • 对于已知分布的总体，若对于某先验分布，得到的后验分布与先验分布同族，则称该先验分布为该总体分布的共轭先验分布

区间估计

1. 概念
   P\left(\hat{\theta}_L \le \theta \le \hat{\theta}_U\right) \ge1-\alpha
   • \left[\hat{\theta}_L, \hat{\theta}_U\right]是\theta的1-\alpha置信区间，若取等则称为同等置信区间，\hat{\theta}_L, \hat{\theta}_U称为\theta的(双侧)置信下限和置信上限
     P\left(\hat{\theta}_L \le \theta \right) \ge1-\alpha
   • \hat{\theta}_L称为\theta的(单侧)置信下限，若取等则称为同等置信下限
     P\left(\hat{\theta}_U \ge \theta \right) \ge1-\alpha
   • \hat{\theta}_U称为\theta的(单侧)置信上限，若取等则称为同等置信上限
2. 枢轴量法
   • 枢轴量: 表达式包含未知参数，但分布与未知参数无关
   • 构造一个枢轴量G(\boldsymbol x,\theta)
   • 找到两个常数c,d，使得
     P(c\le G\le d)=1-\alpha
   • 恒等变形解出参数，得到
     P\left(\hat{\theta}_L \le \theta \le \hat{\theta}_U\right) \ge1-\alpha
   • 对c,d进行选择时，一般是要求使得E(\hat{\theta}_L -\hat{\theta}_U)即可能短，或者是使得
     P\left(G \le c \right) =P\left(G \ge d \right)=\frac{\alpha}{2}
   • 这样得到的置信区间称为等尾置信区间
3. 正态总体下的置信区间
   • 根据估计量的分布构造枢轴量
4. 大样本下的置信区间
   • 根据渐近正态性，构造G(\boldsymbol x,\theta)
   • 利用G(\boldsymbol x,\theta)，构造等尾置信区间
5. 其它
   • 若\theta的置信区间为[\theta_1,\theta_2]，则g(\theta)的置信区间为[g(\theta_1),g(\theta_2)]

假设检验

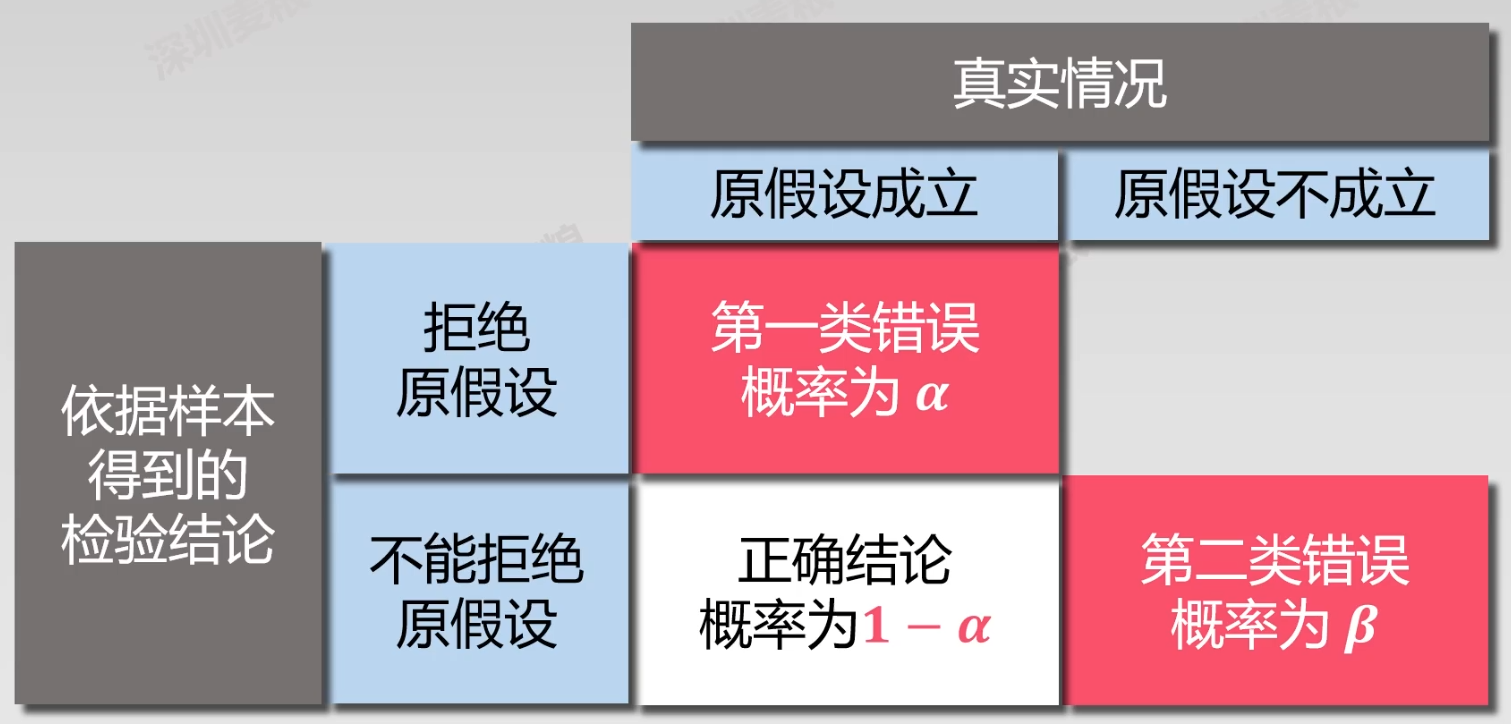
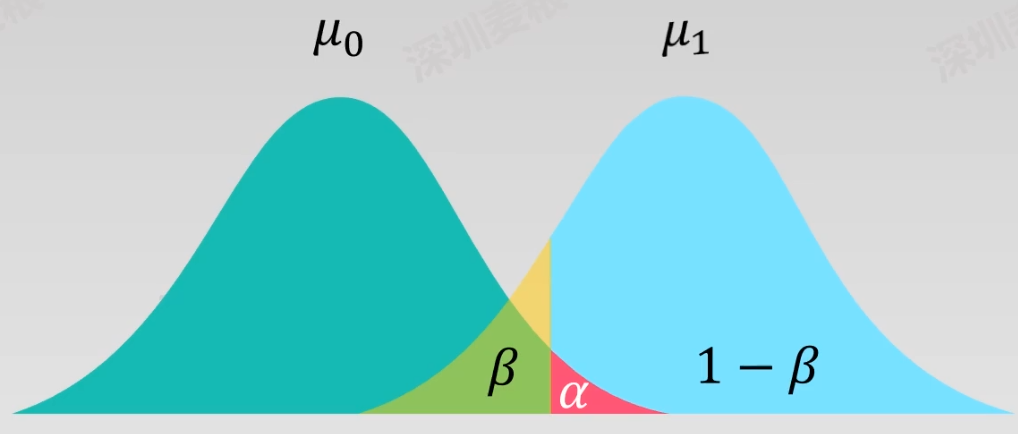
一二类错误

1. 第一类错误\alpha：拒真
   \alpha=P(T(x_1,\cdots,x_n)\in {W_0}\mid H_0)
2. 第二类错误\beta：存伪
   \beta=P(T(x_1,\cdots,x_n)\not\in W_0\mid H_1)
3. 势函数/功效函数
   g(p)=P(T(x_1,\cdots,x_n;p)\in W_0\mid p)
   • 等于1-\beta(p)
     

分布参数检验

1. 原假设假设要检验的量等于某个值
2. 根据该假设的量与样本统计量，存在一个分布，计算该分布的值
3. 若该值落在该分布的拒绝域则拒绝原假设

似然比检验

1. 似然比
   \begin{align} & H_0: \theta \in \Theta_0\quad \text { vs } \quad H_1: \theta \in \Theta_1=\Theta-\Theta_0 \\\\ &\Lambda\left(x_1, x_2, \cdots, x_n\right)=\frac{\sup_{\theta \in \Theta} p\left(x_1, x_2, \cdots, x_n ; \theta\right)}{\sup_{\theta \in \Theta_0} p\left(x_1, x_2, \cdots, x_n ; \theta\right)}=\frac{\sup_{\theta \in \Theta} L\left(\theta\right)}{\sup_{\theta \in \Theta_0} L\left(\theta\right)} \end{align}
   • 定义\Lambda为似然比检验统计量
   • \Lambda满足2\ln\Lambda\dot{\sim}\chi^2(k)，其中k为\Lambda中独立参数个数
   • 如果除了\theta还有其它未知参数，在计算两个上限时令对其它参数偏导为零解得这些参数，再代入
2. 似然比检验
   • 当\Lambda过大时， \theta \in \Theta_0的可能性很小，拒绝原假设
   • 利用2\ln\Lambda\dot{\sim}\chi^2(k)判断是否落在拒绝域

拟合优度检验

1. 分类数据的拟合优度检验
   • 设总体被分成r类，样本中各类个数分别为n_1，原假设为各类的概率为P(A_i)=p_i，此时有
     \sum_{i=1}^r \frac{\left(n_i-n p_{i}\right)^2}{n p_{i}}\xrightarrow{L}\chi^2(r-1)
   • 检验统计量越大越拒绝，利用\chi^2(r-1)判断是否落在拒绝域
   • 似然比检验与拟合优度检验的等价性
     \Lambda\left(x_1, x_2, \cdots, x_n\right)\rightarrow \sum_{i=1}^r \frac{\left(n_i-n p_{i}\right)^2}{n p_{i}}
   • 若p_i之间还额外依赖k个参数，则
     \sum_{i=1}^r \frac{\left(n_i-n p_{i}\right)^2}{n p_{i}}\xrightarrow{L}\chi^2(r-k-1)
2. 分布的拟合优度检验
   • 将样本数据分组，使得每组数据个数大于5并得到各段的区间
   • 利用假设的分布函数得到各区间的假设概率，转化为分类数据的拟合优度检验
   • 若分布包含未知数，用矩估计或最大似然估计计算未知数
3. 列联表独立性检验
   • 相当于二维的分类数据的拟合优度检验
     \sum_{i=1}^r \sum_{j=1}^c \frac{\left(n_{i j}-n {p}_{i j}\right)^2}{n {p}_{i j}}\xrightarrow{L}\chi^2((r-1)(c-1))
   • 检验统计量越大越拒绝，利用\chi^2((r-1)(c-1))判断是否落在拒绝域
   • 特别的，对于2×2列联表
     \frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}\sim \chi^2(1)

回归分析

方差分析

1. 总偏差平方和: S_T=\sum(y_i-\bar y)^2
2. 回归平方和: S_R=\sum(\hat y_i-\bar y)^2
3. 残差平方和: S_e=\sum(y_i-\hat y_i)^2
4. 平方和分解式： S_T=S_R+S_e

一元线性回归

1. 定义: y_i=\beta_0+\beta_1x_i+\varepsilon_i
   \begin{align} &\hat y=\hat\beta_0+\hat\beta_1 x \\ &\hat\beta_1=\frac{Cov(X,Y)}{Var(X)}=\frac{\overline{xy}-\bar x\bar y}{\overline{x^2}-{\bar x}^2}\quad\quad\hat\beta_0=\bar{y}-\hat\beta_1\bar x \end{align}
2. 性质
   \begin{align} &{Cov}\left(\hat{\beta}_0, \hat{\beta}_1\right)=-\frac{\bar x}{ Var(X)}\frac{\sigma^2}{n} \\ &\hat{\beta}_0\sim N\left(\beta_0,\left[1+\frac{{\bar x}^2}{Var(X)}\right]\frac{\sigma^2}{n} \right) \\ &\hat{\beta}_1\sim N\left(\beta_1, \frac{1}{Var(X)}\frac{\sigma^2}{n}\right) \\ &\hat{\beta}_0+\hat{\beta}_1x_0\sim N\left(\beta_0+\beta_1x_0, \left[1+\frac{\left(x_0-\bar{x}\right)^2}{Var(X)}\right] \frac{\sigma^2}{n}\right) \\ & S_e\sim\sigma^2\chi^2(n-2) \\ & S_R=nVar(x)\hat\beta_1^2\sim\sigma^2N^2(\beta_1,1) \end{align}
3. 显著性检验
   • F检验: H_0:\beta_1=0，单侧检验，过大拒绝
     F=\frac{S_R}{S_e/(n-2)}\sim F(1,n-2)
   • t检验: H_0:\beta_1=0，双侧检验
     t=\frac{\hat\beta_1\sqrt{nVar(X)}}{\sqrt{S_e/(n-2)}}\sim t(n-2)
   • 相关系数检验: H_0:\rho=0，单侧检验，过小拒绝
     r=\left|\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}\right|\sim \sqrt\frac{F(1,n-2)}{F(1,n-2)+(n-2)}
     或者t=r\sqrt\frac{n-2}{1-r^2}\sim t(n-2)，此时为双侧检验
4. 估计: 给定x_0时，寻求E(y_0)=\beta_0+\beta_1x_0的估计
   \begin{align} \because\quad&\begin{cases} &\hat{y}_0-E(y_0)\sim N\left(0, \left[1+\frac{\left(x_0-\bar{x}\right)^2}{Var(X)}\right] \frac{\sigma^2}{n}\right) \\ & S_e\sim\sigma^2\chi^2(n-2) \end{cases} \\ \therefore\quad&\frac{(\hat y_0-E(\hat y_0))/\sqrt{\left[1+\frac{\left(x_0-\bar{x}\right)^2}{Var(X)}\right] \frac{\sigma^2}{n}}}{\sqrt{\frac{S_e}{\sigma^2}/(n-2)}}=\frac{\hat y_0-E(\hat y_0)}{\hat\sigma\sqrt{\left[1+\frac{\left(x_0-\bar{x}\right)^2}{Var(X)}\right] \frac{1}{n}}}\sim t(n-2) \\ \text{其中}\quad&\hat\sigma=\sqrt{S_e/(n-2)} \end{align}
   • 因此E(y_0)点估计为\hat y_0，置信区间为\hat y_0\pm t_{1-\alpha/2}(n-2)\hat\sigma\sqrt{\left[1+\frac{\left(x_0-\bar{x}\right)^2}{Var(X)}\right] \frac{1}{n}}
5. 预测: 给定x_0时，寻求y_0的可能区间
   y_0-\hat{y_0}=E(y_0)+\varepsilon-\hat{y_0}\sim N\left(0, \left[1+n+\frac{\left(x_0-\bar{x}\right)^2}{Var(X)}\right] \frac{\sigma^2}{n}\right)
   • 因此y_0最可能取值为\hat y_0，可能取值范围为\hat y_0\pm t_{1-\alpha/2}(n-2)\hat\sigma\sqrt{\left[1+n+\frac{\left(x_0-\bar{x}\right)^2}{Var(X)}\right] \frac{1}{n}}

注意事项

1. t分布求参数，注意参数可能有正负
2. 根据对称性解题
3. 分布函数F(x)，还是概率密度函数f(x)
4. 显著性水平\alpha，还是置信水平(置信度)1-\alpha
5. 同一个对象不同状态，用成对数据检验
6. 均值为还是参数为
7. 求范围，利用P(AB)\in[\max(0,P(A)+P(B)-1),\min(P(A),P(B))]
8. 置信区间要么包含参数，要么不包含参数
9. 假设检验
   • 题目判断什么，什么就是备择假设
   • 如果备择假设成立，对应的估计量相应变动，导致检验量的变动方向为拒绝方向