投资学知识点

金专>金融学
realhuhu 391 0

利率

利率公理化

  1. 利率的频次m：表示一年付息几次，为整数，记为^mr
    • 有效年利率^1r：又记作EAR，非连续复利时，绝大多数利率默认为此利率
    • 名义年利率^kr：又记作APR，k为付息频次，YTM、票息率、非连续复利即期利率套算的远期利率为此利率
    • 名义期利率\frac{^kr}{k}：直接根据两时间点计算出的利率。进行非连续复利计算用的一定是名义期利率（复利法则），有效年利率的名义期利率就是自己，连续复利率的名义期利率为0
    • 连续复利率^\infty r：连续复利时，利率默认为此利率。连续复利即期利率套算的远期利率为此利率
  2. 不同频次利率的转化公式
    \left(1+\frac{^ar}{a}\right)^a=\left(1+\frac{^br}{b}\right)^b=e^{^\infty r}
  3. 时间价值
    • 复利法则：期初本金为A，T时刻后本金变为
      A\left(1+\frac{^mr}{m}\right)^{mT}
    • 例如，期初本金为100，年利率为10%，则2年后本金为
      FV=PV\left(1+ ~^1r\right)^2=121
      或者，计算频次为2的利率再计算终值
      \begin{align} \because\quad&1+ ~^1r=\left(1+ \frac{^2r}{2}\right)^2 \\ \therefore\quad&^2r=9.76\% \\ \therefore\quad&FV=PV\left(1+ \frac{^2r}{2}\right)^4=121 \end{align}
      此外有无数种算法，结果均为121
  4. 连续复利时的有效年利率^1r
    \begin{align} &1+~^1r=\lim_{n\rightarrow +\infty}\left(1+ \frac{^nr}{n}\right)^n=e^{^\infty r} \\ &^1r=e^{^\infty r}-1 \end{align}

    • 例如，期初本金为100，年利率为10%，连续复利，则半年后本金为
      直接利用连续复利计算
      FV=PVe^{^\infty rT}=105.13
      或者化为有效年利率
      \begin{align} &^1r=e^{^\infty r}-1=10.52\% \\ &FV=PV(1+~^1 r)^{0.5}=105.13 \end{align}
      同样的，利用利率频次的转化公式可以得到无数计算方法

通货膨胀

  1. 考虑通货膨胀时利率分为
    • 名义利率_\pi r：未消除通货膨胀的影响的利率
    • 实际利率r：考虑通货膨胀修正后的利率
  2. 注意，这里的名义和名义年利率的名义完全没有关系
    • 名义名义年利率：_\pi^1 r
    • 实际名义年利率：^1 r
    • 名义连续复利率：_\pi^\infty r
    • 实际连续复利率：^\infty r
  3. 名义利率与实际利率转化公式
    \begin{align} \because\quad & (1+ ~^1r)(1+\pi)=(1+ ~^1_\pi r) \\ \therefore\quad & _\pi^1 r= ^1r+\pi+~^1r\pi \\ & ^1r=\frac{1+~^1_\pi r}{1+\pi} -1 \end{align}

    • 注意：通胀率的频次为1，名义利率的频次不为1时，必须转化为有效年利率计算实际利率，再转为原频次
    • 因此，有效年利率是枢纽，既可以调整频次，又可以调整通胀
  4. 名义现金流与实际现金流转化公式
    • 现金流：名义值等价于实际值按\pi复利
      _\pi CF_t=CF_t(1+\pi)^t
    • 终值：名义值等价于实际值按\pi复利
      \begin{align} _\pi FV&=\sum_{t=1}^{T}{~_\pi CF_t(1+~_\pi r)^{T-t}} \\ &=\sum_{t=1}^{T}{CF_t(1+\pi)^t(1+r)^{T-t}(1+\pi)^{T-t}} \\ &=(1+\pi)^{T}\sum_{t=1}^{T}{CF_t(1+r)^{T-t}} \\ &=FV(1+\pi)^{T} \end{align}
    • 现值：名义值等于实际值
      \begin{align} _\pi PV&=\sum_{t=1}^{T}\frac{~_\pi CF_t}{(1+~_\pi r)^{t}} \\ &=\sum_{t=1}^{T}\frac{ CF_t(1+\pi)^t}{(1+ r)^{t}(1+\pi)^t} \\ &=\sum_{t=1}^{T}\frac{ CF_t}{(1+ r)^{t}} \\ &=PV \end{align}
    • 终值与现值：用对应利率复利
      \begin{align} &_\pi FV= ~_\pi PV(1+~_\pi r)^T \\ &FV= PV(1+ r)^T \end{align}

年金因子

  1. 现值因子
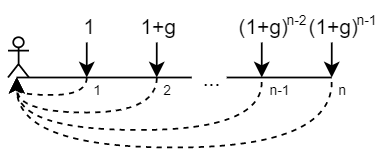
    投资学知识点

    • 计算公式
      \mathrm{PVIFA}_{r,n,g}=\frac{1}{r-g}\left[1- \left(\frac{1+g}{1+r}\right)^{n}\right]
    • 将n期名义期利率为r，以g为增长率的、第一期为1的现金流折现到前一期
  2. 终值系数
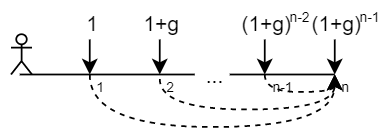
    投资学知识点

    • 计算公式
      \mathrm{FVIFA}_{r,n,g}=\frac{1}{r-g}\left[(1+r)^{n}-(1+g)^n\right]
    • 将n期名义期利率为r、以g为增长率的、第一期为1的现金流折现到最后一期
  3. 若付息频次为k，则
    \begin{align} &\mathrm{PVIFA}_{r,n,g}=\frac{1}{~^kr-~^kg}\left[1- \left(\frac{1+~^1g}{1+~^1r}\right)^{n}\right] \\ &\mathrm{FVIFA}_{r,n,g}=\frac{1}{~^kr-~^kg}\left[(1+~^1r)^{n}-(1+~^1g)^n\right] \end{align}

收益率

  1. 持有期收益率: (资本利得 + 全部利息) / 期初投资
  2. 资本利得率: 资本利得 / 期初投资
  3. 当期收益率：一年利息 / 期初投资
  4. 赎回收益率: 使得期初到赎回期间的利息、赎回价格折现后等于期初债券价值的折现率
  5. 到期收益率（复利）: 使得购入到到期期间的现金流折现后等于购入价格的折现率
  6. 到期收益率（单利）: 忽略时间价值计算的收益率 / 总年数

金融产品

债券

久期

  1. 麦考利久期D：收回成本的平均时间
    D = \frac{\sum \frac{t\cdot CF_t}{(1+y)^t}}{\sum \frac{ CF_t}{(1+y)^t}}=\frac{1}{P}{\sum \frac{t\cdot CF_t}{(1+y)^t}}=\sum t\cdot\frac{PV_t}{P}

    • y为名义期利率
    • 永续债券的麦考利久期：\frac{1+y}{y}
  2. 修正久期D^\ast：债券价格变动率与YTM变动率之比
    D^\ast=-\frac{\frac{\mathrm d P}{P}}{\mathrm d y}=\frac{D}{1+y}= \frac{1}{1+y}\sum t\cdot\frac{PV_t}{P}

    • y为名义期利率
    • 永续债券的修正久期：\frac{1}{y}
  3. 有效久期
    \text{有效久期}=-\frac{\Delta P/P}{\Delta r}

    • 计算隐含期权金融工具的久期
  4. 久期法则
    \frac{\Delta P}{P}=-D^\ast\cdot\Delta y

凸度

  1. 公式
    C=\frac{1}{P}{\sum \frac{t\cdot(t+1)\cdot CF_t}{(1+y)^{t+2}}}=\frac{1}{(1+y)^2}\sum t\cdot(t+1)\cdot\frac{PV_t}{P}
  2. 久期凸度法则
    \frac{\Delta P}{P}=-D^\ast\cdot\Delta y+\frac{1}{2}\cdot C\cdot(\Delta y)^2

股票

  1. 基本公式：DDM
    P_0=\sum_{i=1}^n \frac{D_i}{(1+r)^i}+\frac{P_n}{(1+r)^n}=\sum_{i=1}^{\infty} \frac{D_i}{(1+r)^i}

    • 零增长：P_0=\frac{D}{r}
    • 固定增长率g：P_0=\frac{D_0(1+g)}{r-g}=\frac{D_1}{r-g}
  2. 增长率g
    • 假设以前的项目的现金流不变，留存收益投资项目的收益率为ROE，则
      NI_1=NI_0+RE\times ROE\quad\Rightarrow\quad g=b\times ROE
    • 此时股价
      P_0=\frac{D_0(1+g)}{r-g}=\frac{EPS_0(1-b)(1+b\times ROE)}{r-b\times ROE}
    • 其他条件不变时，由于NI以g增长，D与P也以g增长
  3. 收益率r
    P_0=\frac{D_0(1+g)}{(r-g)(1-f)}\quad\Rightarrow\quad r=\frac{D_0(1+g)}{P_0(1-f)}+g

    • 同时还是股票的一年期HPY
  4. 增长机会价值PVGO
    \begin{align} \because\quad&P_0=\frac{EPS_1}{r}+PVGO \\ \therefore\quad&PVGO=\frac{EPS_1(1-b)}{r-g}-\frac{EPS_1}{r}=\frac{EPS_1}{r}\frac{b}{r-g}(ROE-r) \end{align}

    • 注意用的是下一期的股利
    • 当留存收益的投资回报率大于市场利率，投资才能增加股价
  5. 常见表述
    • 今年每股收益为 → EPS_0
    • 预期每股收益为 → EPS_1
    • 刚刚派发股利 → P_0不需要加上EPS_0

远期

  1. 构建两个组合，组合1持有资产，组合2持有一份远期合约和现金
    • 使得二者现金流相同，求出价值
    • 令远期机制为零，求出交割价格
      类别 估值f_t 定价F_t
      无收益 f_t=S_t-Ke^{-r(T-t)} F_t=S_te^{r(T-t)}
      连续收益率q f_t=S_te^{-q(T-t)}-Ke^{-r(T-t)} F_t=S_te^{(r-q)(T-t)}
      现金收益I_t f_t=S_t-I_t-Ke^{-r(T-t)} F_t=(S_t-I_t)e^{r(T-t)}
    • I_t为t时刻之后现金收益的折现值之和
  2. 估值与定价的意义
    • 估值：表示以K为协议价格的远期合约在t时刻的价值
    • 定价：表示在t时刻使双方不盈利不亏损的协议价格K
  3. 估值、定价、协议价格的关系
    f_t=(F_t-K)e^{-r(T-t)}

    • 若t时刻理论价格大于协议价格则多头盈利，表现为估值为正，盈利的现值就是f_t
  4. 远期价格的期限结构
    • 不同T下的F_t与T的关系
      \begin{align} \because\quad&\begin{cases} &F_t(T_1)=Se^{z_1(T_1-t)}\\ &F_t(T_2)=Se^{z_2(T_2-t)} \end{cases} \\ \therefore\quad& F_t(T_2)=F_t(T_1)e^{z_2(T_2-t)-z_1(T_1-t)}=F_t(T_1)e^{f_{1,2}(T_2-T_1)} \end{align}
    • 恰好为按远期利率复利

FRA

  1. 远期利率协议的定价与估值
    • 对于市场远期利率\mathcal{F}和协议远期利率\mathcal{K}的FRA，其价值就是t_2时刻净现金流在t_0的现值，即
      V=Ae^{-r(t_2-t_0)}\left[e^{\mathcal{F}_{t_1,t_2}(t_2-t_1)}-e^{\mathcal{K}(t_2-t_1)}\right]
    • 若不为连续复息，则为
      V=\frac{A(\mathcal{F}_{t_1,t_2}-\mathcal{K})(t_2-t_1)}{1+r(t_2-t_0)}
      注意t_2-t_0为一年的百分比形式
    • 若使得价值为0，求出的\mathcal{K}就是t_0时刻FRA的价格
  2. 远期利率协议的结算金
    • 在t_1时刻，此时r与\mathcal{F}_{t_1,t_2}已确定，可以结算FRA的净值
      \begin{align} S & =Ae^{-r(t_2-t_1)}\left[e^{r(t_2-t_1)}-e^{\mathcal{K}(t_2-t_1)}\right]\\ & =A\left[1-e^{(\mathcal{K}-r)(t_2-t_1)}\right] \end{align}
    • 若不为连续复息，则为
      S=\frac{A(r-\mathcal{K})(t_2-t_1)}{1+r(t_2-t_1)}
      注意t_2-t_1为一年的百分比形式
  3. 购买远期利率协议后，实际借款成本锁定为\mathcal{K}
    • 预期未来利率上升，买入FRA，利率上升时获益
    • 预期未来利率下降，卖出FRA，利率下降时获益

期货

国债期货

  1. 净价和全价
    • 净价(报价) = 全价(现金价格) - 应计利息
    • 应计利息 = 区间利息 × 区间已经经过的百分比
    • 净价为未来现金流折现和，全价才是实际支付的现金
  2. 转换因子
    • 把其它债券现货转换为标准债券期货，使得不同债券具有可比性。普通债券 = 转换因子 × 标准债券
    • 转换因子的计算： 面值一元的该债券的未来现金流按6%收益率（半年付息）贴现再扣除应计利息后的余额
    • 剩余期限以3个月为单位向下取整，若剩余期限不为半年的倍数则会有应计利息
  3. 发票金额
    • 交割券现货发票金额 = 标准券期货报价 × 交割券转换因子 + 应计利息（面值要相同）
    • "标准券期货报价 × 交割券转换因子"为报价，"应计利息"用于补偿卖方持有期间的利息
  4. 最便宜可交割债券
    • 卖方收入: 标准券期货报价 × 交割券转换因子 + 应计利息
    • 卖方成本: 交割券现货报价 + 应计利息
    • 卖方交割成本: 交割券现货报价 - 标准券期货报价 × 交割券转换因子
    • 选择交割成本最低的进行交割
  5. 长期国债期货合约定价：假设最便宜可交割债券和交割日期已知
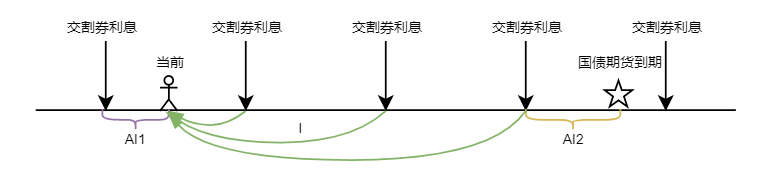
    投资学知识点

    • 根据交割券现货净价计算出交割券现货全价
      S_D = S_C + AI_1
    • 根据交割券现货全价计算出交割券期货全价
      F_D=(S_D-I)e^{r(T-t)}
    • 根据交割券期货全价计算出交割券期货净价
      F_C=F_D-AI_2
    • 交割券期货净价除以转换因子就是标准券期货报价
      P_C=\frac{F_C}{CF}
    • I为国债期货到期日前交割券利息现值，AI_1为当前到上次付息，AI_2为国债期货到期日到上次付息

外汇期货

  1. 报价形式
    • 单向：1EUR=1.2USD
    • 双向: 1EUR=1.2/1.21USD，1.2为卖出价、1.21为买入价
  2. 外汇期货：到期以约定汇率收到外币
    • 到期时间：期货最终交割时间
    • 交易单位: 购买一单位外汇期货需要的本币价格，欧元期货为12.5万，日元期货为1250万，美元期货为7.35万
    • 价格（间接标价法）: 表示人们对汇率的预期，形式为本币/外币=xxx，或简写为外币xxx，或简写为xxx（默认外币为美元）
    • 例如：2024年12月欧元期货价格1.087，表示花费12.5万欧元购买1单位期货后，在2024年12月能收到
      125000\times 1.087=135875(\text{USD})
  3. 外汇期货的平仓：提前收回本币
    • 外汇期货购买后不一定必须等到交割，也可以提前平仓，收回本币
    • 每单位期货的收益 = 交易单位 × 价格的变动
    • 例如：当前12月期欧元期货价格为USD1.1062，一个月后该欧元期货价格为USD1.1736，则每份期货收益为
      125000\times(1.1736-1.1062)=8425 (\text{GBP})
  4. 外汇期货的定价与估值（直接标价法）
    \begin{align} &F_t=Se^{(r-r^\ast)(T-t)} \\ &f_t=(F_t-K)e^{-r(T-t)} \end{align}

    • 相当于连续收益率为外币利率的有收益期货
  5. 策略
    • 认为货币将升值则买入该货币期货
    • 认为货币将贬值则卖出该货币期货

互换

  1. 利率互换

    • 对于固定利息支付方（多头），V_{swap}=B_{float}-B_{fix}；对于浮动利息支付方（空头），V_{swap}=B_{fix}-B_{float}
    • 将固定利息的现金流折现得到B_{fix}；将浮动利息的现金流折现得到B_{float}
      \begin{aligned} & B_{{fix }}=\sum_{i=1}^n k_i e^{-z_i t_i}+A e^{-z_n t_n} \\ & B_{ {flow }}=\left(A+k^\ast\right) e^{-z_1t_1} \end{aligned}
      若付息利率为连续复利，需要转化为对应频次的APR利率再计算固定债券和浮动债券的利息
      k_i为未来第i期的固定现金流，k^\ast为下一期浮动现金流，z_i为当下到未来第i期时刻t_i的即期LIBOR（连续复利）
      固定债券的价值等于未来现金流的现值和，浮动债券的价值在付息下时刻等于面值
      上一时刻的名义期LIBOR决定当前的浮动利息，用即期LIBOR套算远期LIBOR，再调整频次得到
    • 或者将每个时刻的利息流入流出当成FRA，计算一系列FRA的现值求出互换价值
      V=A\sum_{i=1}^n e^{-\mathcal{z}_it_i}\left[e^{\mathcal{K}(t_i-t_{i-1})}-e^{\mathcal{f}_{t_{i-1},t_i}(t_i-t_{i-1})}\right]
      \mathcal{K}固定端利率（连续复利）
      \mathcal{f}_{t_{i-1},t_i}为t_{i-1}到t_i的远期利率，公式为（即期利率需要为连续复利）
      \mathcal{f}_{t_{i-1},t_i}=\begin{cases} & \mathcal{z}_1 &i=1\\ & \frac{\mathcal{z}_{t_i}t_i-\mathcal{z}_{t_{i-1}}t_{i-1}}{t_{i}-t_{i-1}} &i\gt 1 \end{cases}
    • 令V等于0即可给利率互换定价
      A\sum_{i=1}^n e^{-\mathcal{z}_it_i}\left[e^{\mathcal{K}(t_i-t_{i-1})}-e^{\mathcal{f}_{t_{i-1},t_i}(t_i-t_{i-1})}\right]=0\quad\Rightarrow\quad\mathcal{K}
      若按年复利，每年年末交换现金
      \begin{align} \because\quad&A\sum_{i=1}^n \frac{\mathcal{K}-\mathcal{f}_{{i-1},i}}{(1+z_i)^{i}}=0 \\ \therefore\quad&\mathcal{K}=\frac{\sum_{i=1}^n \frac{1+\mathcal{f}_{{i-1},i}}{(1+z_i)^{i}}}{\sum_{i=1}^n \frac{1}{(1+z_i)^{i}}}-1=\frac{\sum_{i=1}^n \frac{1}{(1+z_{i-1})^{i-1}}}{\sum_{i=1}^n \frac{1}{(1+z_i)^{i}}}-1=\frac{\sum_{i=1}^n B_{i-1}}{\sum_{i=1}^n B_i}-1 \end{align}
      其中B_i为期限为i年的零息债的价值
    • 注意事项
      互换利率为整年的利率，若多次付息要平均
      以前的LIBOR确定浮动利息，零时刻LIBOR折现浮动利息

  2. 货币互换

    • 对于收本币付外币，V_{swap}=B_{D}-S_0B_{F}；对于收外币付本币，V_{swap}=S_0B_{F}-B_{D}
    • 将未来现金流用对应货币的利率折现，再用当前汇率换算成同一货币，即为互换价值
      \begin{align} &B_{D}=\sum_{i=1}^n k_{D,i} e^{-z_{D,i} t_i}+A_D e^{-z_{D,n} t_n} \\ &B_{F}=\sum_{i=1}^n k_{F,i} e^{-z_{F,i} t_i}+A_F e^{-z_{F,n} t_n} \end{align}
      假设初始汇率A/B=S_0，则货币A为外币，B为本币
      若付息利率为连续复利，需要转化为对应频次的APR利率再计算国内债券和国外债券的利息
      k_i为未来第i期的国内/国外现金流，z_i为当下到未来第i期时刻t_i的即期货币利率（连续复利）
    • 或者将每个时刻的利息流入流出当成FRA，计算一系列FRA的现值求出互换价值
      \begin{align} &S_i=S_0 e^{(z_{D,i}-z_{F,i})t_i} \\ &V=\sum_{i=1}^n\left(S_i k_{F,i} - k_{D,i}\right)e^{-z_{D,i} t_i}+\left(S_n A_F - A_D\right) e^{-z_{D,n} t_n} \end{align}
      S_i为t_i时刻的远期汇率
      将所有FRA折算为本币，用本币即期利率折现求和，得到互换价值
    • 互换比率：在t_0\sim t_n期间支付n次金额为Q的外币，则需要收到n次金额为QR_n的本币，R_n就是互换比率
      V=\sum_{i=1}^n\left(S_i Q - R_nQ\right)e^{-z_{D,i} t_i}=0\quad\Rightarrow\quad R_n=\frac{\sum_{i=1}^n S_i e^{-z_{D,i} t_i}}{\sum_{i=1}^n e^{-z_{D,i} t_i}}=\frac{\sum_{i=1}^n e^{-z_{F,i} t_i}}{\sum_{i=1}^n e^{-z_{D,i} t_i}}S_0
      表明R_n是远期汇率根据本币利率加权得到的一种特殊汇率
      一期的互换比率R_1实际上就是远期汇率
      如果有抛补，S_i就不是远期汇率而是远期外汇的价格

期权

期权的价值

  1. 期权费
    • 如果要考虑时间价值，则复利后的期权费才是真正的期权费，协议价格不变
    • 期权费可能为a%形式，此时盈亏平衡点为(1±a%)×协议价格，倒算出期权费
    • 外汇期权期权费表示为汇率可能双重报价，外币换本币用左价，本币换外币用后价。支付的期权费就是用期权费作为汇率换算出的面额
  2. 期权价值 = 绝对内在价值 + 时间价值
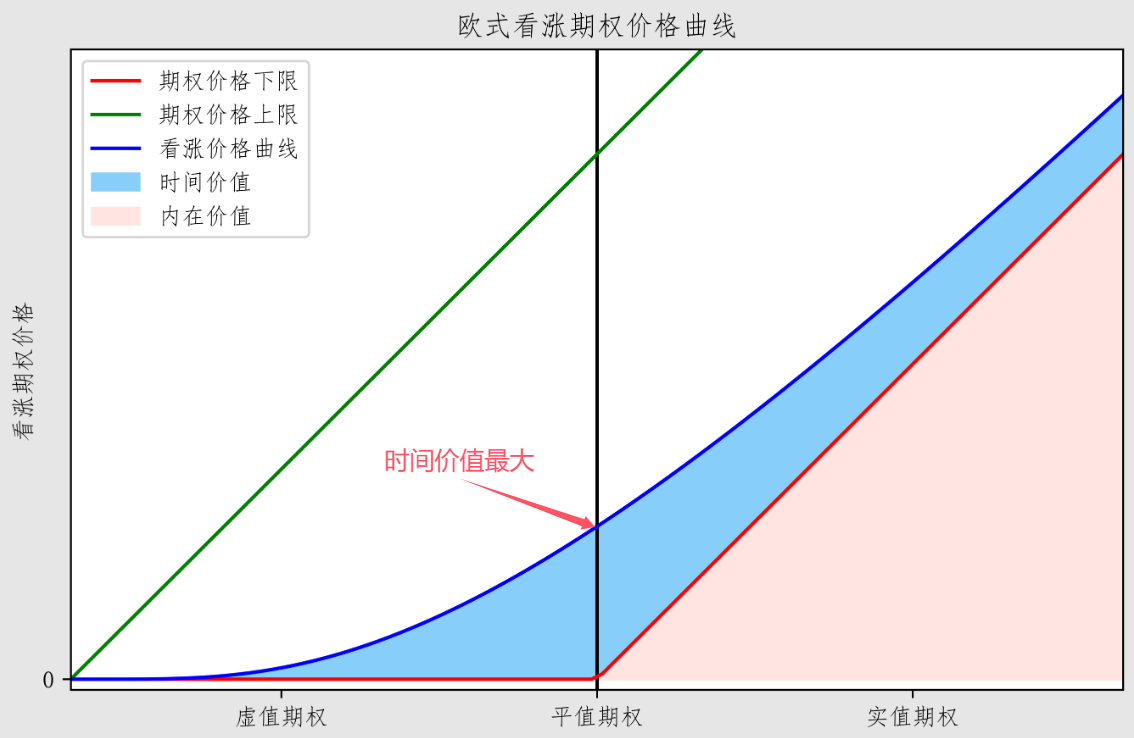
    投资学知识点

    • 内在价值：所有可行权时间点中行权收益现值最大的那个贴现值，随时间波动
      有的地方将本文中内在价值与0中较大者作为内在价值，本文称其为绝对内在价值
    • 时间价值：由于标的物价格变动导致期权价值增加的可能性，随直接递减到0，也是贴现值
      时间价值在期权实值的时候最高
    • 其它条件相同的看涨期权和看跌期权具有相同时间价值
  3. 期权的内在价值
    分类 可行行权时点与价值 内在价值
    看涨期权 欧式 无收益 V_T=S_T-X S_0-Xe^{-rT}
    有收益 V_T=S_T-I_T(T)-X S_0-I_0(T)-Xe^{-rT}
    美式 无收益 V_T=S_T-X S_0-Xe^{-rT}
    有收益 \begin{aligned} & V_T=S_T-I_T(T)-X\\& V_{\tau_i-}=S_{\tau_i}-I_{\tau_i}(\tau_{i-1})-X\quad(i=1,2,\cdots)\end{aligned} \begin{aligned} & S_0-I_0(T)-Xe^{-rT}\\& S_0-I_0(\tau_{i-1})-Xe^{-r\tau_i}\end{aligned}
    看跌期权 欧式 无收益 V_T=X-S_T Xe^{-rT}-S_0
    有收益 V_T=X-[S_T-I_T(T)] Xe^{-rT}-[S_0-I_0(T)]
    美式 无收益 V_0=X-S_0 X-S_0
    有收益 \begin{aligned} & V_0=X-S_0\\& V_{\tau_i+}=X-[S_{\tau_i}-I_{\tau_i}(\tau_{i})]\quad(i=1,2,\cdots)\end{aligned} \begin{aligned} & X-S_0\\& Xe^{-r\tau_i}-[S_0-I_{0}(\tau_i)]\end{aligned}
    • V_t,V_{t+},V_{t-}表示在时间T、后一时刻、前一时刻行权时的收益，折现后为的现值就是可能的内在价值
    • 假设债券在t=\tau_i派息，\tau_0的派息为0，I_t(\tau)为[0,\tau]时间区间内所有收益复利/折现到t之和
    • 内在价值大于0为实值期权，等于0为平值期权，小于0为虚值期权。到期时只有内在价值大于0才行权
  4. 期权的提前行权
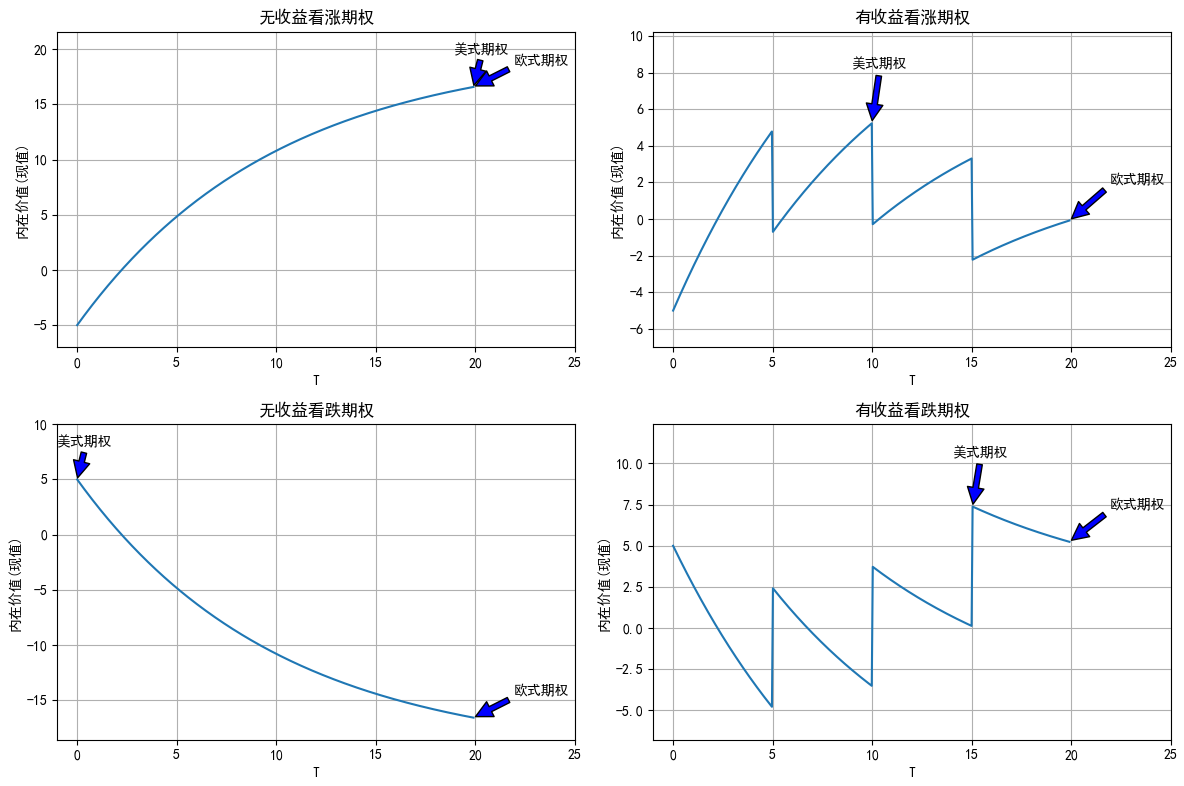
    投资学知识点

    • 由于欧式期权无法提前行权，计算在T时刻行权收益折现后就是内在价值
    • 美式无收益看涨期权一定不提前行权。因为收益现值始终为S_0，提前行权成本现值更大（Xe^{-rt}\gt Xe^{-rT}）
    • 美式无收益看跌期权一定会期初行权。因为成本现值始终为S_0，提前行权收益现值更大（X\gt Xe^{-rt}）
    • 美式有收益看涨期权可能会提前行权（付息日前一刻）。虽然提前行权导致成本现值更大，但也导致收益增大（避免了之后的除息）
      比较不同时刻内在价值，可以得出美式有收益看涨期权在第a次派息前行权而不是第b次派息前行权的条件是(b\gt a)
      X\left[1-e^{-r(\tau_b-\tau_a)}\right]\lt D_{a,b-}\quad D_{a,b-}\text{为}[\tau_a,\tau_b)\text{期间派息折现到}a\text{的现值和}
      令\tau_b=T求出美式有收益看涨期权提前行权的条件为：\exists a使得X\left[1-e^{-r(T-\tau_a)}\right]\lt D_{a,\infty}
    • 美式有收益看跌期权一定会提前行权（期初或付息日后一刻）。首先不可能选择在期末行权，因为在最后一次派息和期末之间，除息后价格现值不变（因为没有派息），而收益却在减少，因此在最后一次派息后一刻行权一定优于不行权。同理在派息下一刻行权一定优于到下一次派息前这段时间行权。
      比较不同时刻内在价值，可以得出美式有收益看跌期权在第a次派息前行权而不是第b次派息前行权的条件是(b\gt a)
      X\left[1-e^{-r(\tau_b-\tau_a)}\right]\gt D_{a+,b}\quad D_{a+,b}\text{为}(\tau_a,\tau_b]\text{期间派息折现到}a\text{的现值和}
      令\tau_a=0求出美式有收益看跌期权不在期初行权的条件为：\exists b使得X\left(1-e^{-r\tau_b}\right)\lt D_{0,b}
  5. 期权的价值上下限
    分类 上限 下限
    看涨期权 欧式 无收益 S_0 \max \left\{S_0-Xe^{-rT},\ 0\right\}
    有收益 S_0-I_0(T) \max \left\{S_0-I_0(T)-Xe^{-rT},\ 0\right\}
    美式 无收益 S_0 \max \left\{S_0-Xe^{-rT},\ 0\right\}
    有收益 \max \left\{S_0-I_0(T)-Xe^{-rT},\ S_0-I_0(\tau_{i-1})-Xe^{-r\tau_i},\ 0\right\}
    看跌期权 欧式 无收益 Xe^{-rT} \max \left\{Xe^{-rT}-S_0,\ 0\right\}
    有收益 \max \left\{Xe^{-rT}-[S_0-I_0(T)],0\ \right\}
    美式 无收益 X \max \left\{X-S_0,\ 0\right\}
    有收益 \max \left\{X-S_0,\ Xe^{-r\tau_i}-[S_t-I_{0}(\tau_i)],\ 0\right\}
    • 由于期权的价值包括绝对内在价值和时间价值，时间价值大于0，因此价值下限就是绝对内在价值
    • 对于看涨期权，价值不可能超过资产价格，因此价格上限就是S，其中欧式期权不能提前行权需要除息
    • 对于看跌期权，价值不可能超过收益上限，因此价格上限就是X，其中欧式期权不能提前行权需要折现
  6. 期权价值的影响因素
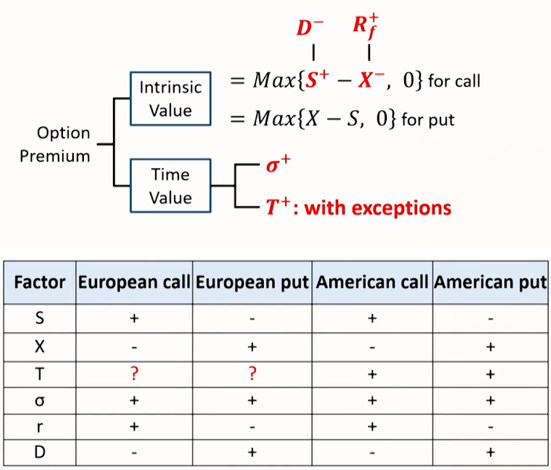
    投资学知识点

    • 对于美式期权，期权有效期越长，行权的机会越多，因此看涨期权价格增加，看跌期权价格减少
    • 对于欧式期权，时间对成本和收益可能有同方向影响（除息和行权价的折现），因此不确定价格的变化
  7. 期权的平价关系
    • 欧式期权：看涨期权价格为c，看跌期权价格为p
      无资产收益
      p+S_0=c+Xe^{-rT}
      有资产收益
      p+[S_0-I_0(T)]=c+Xe^{-rT}
      一般情况
      p+f=c
      其中f为协议价格为X的远期的价值
    • 美式期权：看涨期权价格为C，看跌期权价格为P
      由于美式看涨不提前行权，美式看跌一定提前行权，因此
      C=c,P\ge p\quad\Rightarrow\quad C-P\le c-p
      并且，无论是否提前行权，欧式看涨期权c + 现金X的组合价值总大于美式看跌期权p + 标的资产S，因此
      C-P=c-P\ge S - X
      得到：无资产收益
      S_0-X\le C-P\le S_0-Xe^{-rT}
      有资产收益
      [S_0-I_0(T)]-X\le C-P\le S_0-Xe^{-rT}

期权交易策略

  1. 担保期权
    • 有担保的看涨期权（备兑看涨期权） = 看涨期权空头 + 标的资产多头
      投资学知识点
    • 有担保的看跌期权（备兑看跌期权） = 看跌期权多头 + 标的资产多头
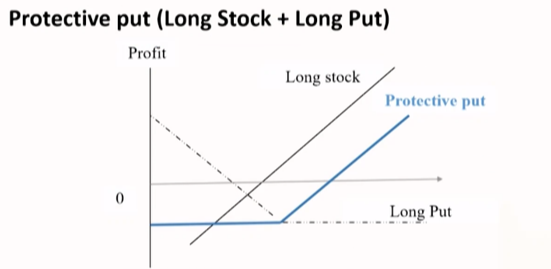
      投资学知识点
  2. 牛市价差
    • 牛市价差组合 = 看涨期权多头 + 更高行权价的看涨期权空头
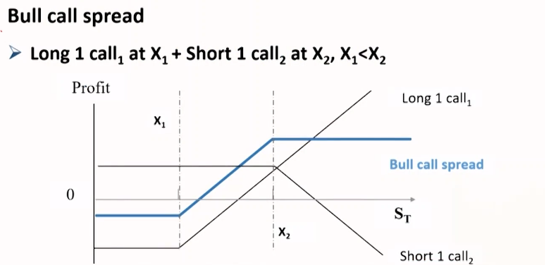
      投资学知识点
    • 牛市价差组合 = 看跌期权多头 + 更高行权价的看跌期权空头
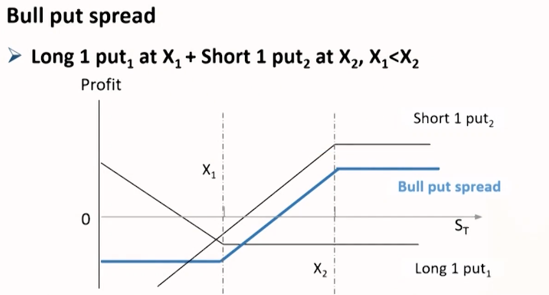
      投资学知识点
    • 牛市价差组合的作用
      预期价格上升但上升幅度不大，以低于看涨期权的成本投资，当然收益也更低
      卖出看跌期权投机于上升预期，之后通过买人一份行权价格较低的看跌期权进行风险管理
      期权相对价格不合理时套利
    • 两种牛市价差组合的区别
      看涨：期初现金流为负，最终收益更大
      看跌：期初现金流为正，最终收益更小
  3. 熊市价差
    • 熊市价差组合 = 看涨期权多头 + 更低行权价的看涨期权空头
      投资学知识点
    • 熊市价差组合 = 看跌期权多头 + 更低行权价的看跌期权空头
      投资学知识点
    • 熊市价差组合的作用
      预期价格下跌但下跌幅度不大，以低于看跌期权的成本投资，当然收益也更低
      卖出看涨期权投机于下跌预期，同时通过买入一份行权价格较高的看涨期权进行风险管理
      期权相对价格不合理时套利
    • 两种熊市价差组合的区别
      看涨：期初现金流为正，最终收益更小
      看跌：期初现金流为负，最终收益更大
  4. 蝶式价差
    • （正向）蝶式价差组合 = 看涨期权多头 + 2看涨期权空头 + 看涨期权多头
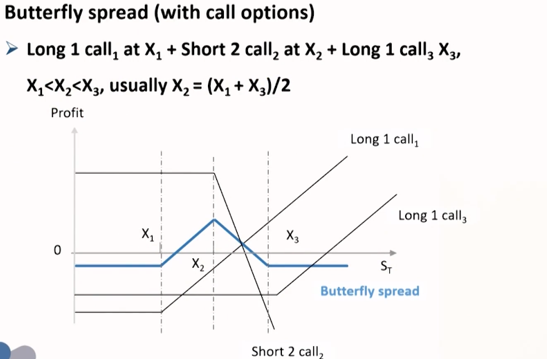
      投资学知识点
    • （正向）蝶式价差组合 = 看跌期权多头 + 2看跌期权空头 + 看跌期权多头
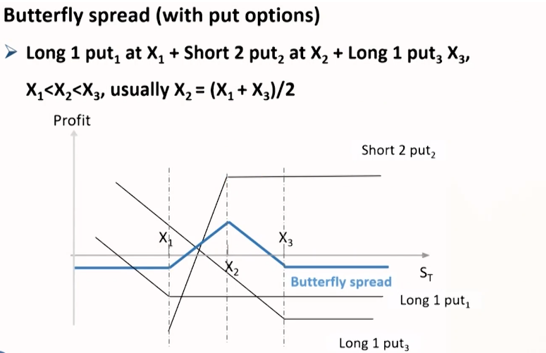
      投资学知识点
    • 蝶式价差组合的作用
      预测价格会在一定区间内波动
    • 两种蝶式价差组合的区别
      无论初始投资还是最终收益都相同
  5. 差期
    • （正向）差期组合 = 看涨期权多头 + 更短期限的看涨期权空头
    • （正向）差期组合 = 看跌期权多头 + 更短期限的看跌期权空头
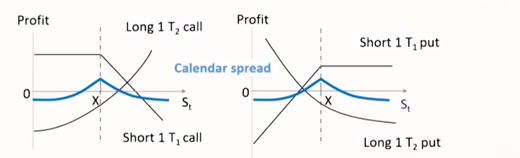
      投资学知识点
  6. 跨式
    • （底部）跨式组合 = 看涨期权多头 + 看跌期权多头
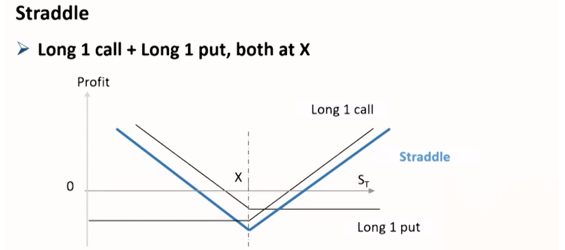
      投资学知识点
    • 预测股价会有重大波动但不知道具体方向，如企业收购

期权的定价

  1. 复制定价法
    • 将一份期权与h^\ast份头寸相反的股票组合，使得无论股价上升到到u倍者下降至d倍，最终现金流收益相同
      f_u-h^\ast Su=f_d-h^\ast Sd\quad\Rightarrow\quad h^\ast=\frac{f_u-f_d}{Su-Sd}
      |h^\ast|为最优对冲比率
    • 于是一份期权加上h^\ast份股票的组合未来现金流确定，等于期初投入的终值
      (f-h^\ast S)e^{rT}=f_u-h^\ast Su=f_d-h^\ast Sd
    • 解出期权价格f
      f=f_u e^{-rT} +h^\ast S\left(1-ue^{-rT}\right)=f_d e^{-rT} +h^\ast S\left(1-de^{-rT}\right)
    • 一般来说f_u,f_d有一个为零
  2. 风险中性定价
    • 假股价上涨到u倍的概率为\hat{\mathbb{P}}，下降到d倍的概率为1-\hat{\mathbb{P}}，于是
      \begin{align} &Se^{r T}=S u \hat{\mathbb{P}}+S d(1-\hat{\mathbb{P}}) \\ &\hat{\mathbb{P}}=\frac{e^{r T}-d}{u-d} \end{align}
    • 期权价格为
      f=e^{-r T}\left[\hat{\mathbb{P}} f_u+(1-\hat{\mathbb{P}}) f_d\right]
    • 若u,d未知，但波动率\sigma已知，则可以求出u,d
      u =e^{\sigma \sqrt{T}} \quad d =e^{-\sigma \sqrt{T}}
  3. BS公式
    • 无收益
      \begin{align} &c=S \mathrm{N}\left(d_1\right)-K {e}^{-rT } \mathrm{N}\left(d_2\right) \\ &p=K {e}^{-rT } \mathrm{N}\left(-d_2\right)-S \mathrm{N}\left(-d_1\right)=c+Ke^{-rT}-S \end{align}
      其中
      \begin{align} & d_1=\frac{\ln (S / K)+\left(r+\sigma^2/2\right) T}{\sigma \sqrt{T}} \\ & d_2=\frac{\ln (S / K)+\left(r-\sigma^2/2\right) T}{\sigma \sqrt{T}}=d_1-\sigma \sqrt{T} \end{align}
    • 有收益
      \begin{align} &c=e^{-rT}\mathrm P(\mathbf S\gt K)\left[\mathrm E(\mathbf S\mid \mathbf S\gt K)-K\right] \\ &p=e^{-rT}\mathrm P(\mathbf S\lt K)\left[K-\mathrm E(\mathbf S\mid \mathbf S\lt K)\right] \end{align}
      由于
      \begin{align} &\mathrm P(\mathbf S\gt K)=\mathrm N(d_2) \\ &\mathrm P(\mathbf S\lt K)=\mathrm N(-d_2) \\ &\mathrm E(\mathbf S\mid S\gt K)=\mathrm E(\mathbf S)\frac{N(d_1)}{N(d_2)}=F\frac{N(d_1)}{N(d_2)} \\ &\mathrm E(\mathbf S\mid S\lt K)=\mathrm E(\mathbf S)\frac{N(-d_1)}{N(-d_2)}=F\frac{N(-d_1)}{N(-d_2)} \\ & d_1=\frac{\ln (F / K)}{\sigma \sqrt{T}}+\frac{\sigma\sqrt T}{2} \\ & d_2=\frac{\ln (F / K)}{\sigma \sqrt{T}}-\frac{\sigma\sqrt T}{2}=d_1-\sigma \sqrt{T} \end{align}
      因此
      \begin{align} &c=e^{-rT}\left[F\mathrm N(d_1)-K\mathrm N(d_2)\right] \\ &p=e^{-rT}\left[K\mathrm N(-d_2)-F\mathrm N(-d_1)\right] \end{align}
      其中，\mathbf S为T时刻期货标的资产价格的概率分布，F为以期货标的资产为标的物、合约期限为T的远期的定价
  4. 注意事项
    • 对于多期二叉树，从后往前依次计算得到每个节点的值，或对每条路径按概率加权求和最后折现
    • 如果是美式期权，比较二叉树结果和直接行权收益，选择大的作为节点值
    • 如果发放股利，先绘制无股利时二叉树，再绘制期初除权后二叉树，在股利日拼接两个二叉树

期权与公司评估

  1. 从看涨期权角度
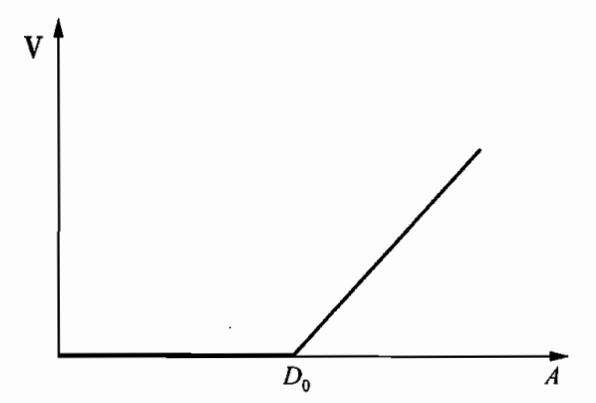
    投资学知识点

    • 权益的价值V_E相当于行权价值为D，当前股价为A的看涨期权
    • V_E=C
      股东从债权人购买了一个看涨期权
    • V_D=A-C，收益率为\frac{D}{V_D}-1，应当小于无风险利率，否则存在债务风险
      债权人拥有公司
      债权人向股东出售了一个看涨期权
  2. 从看跌期权角度
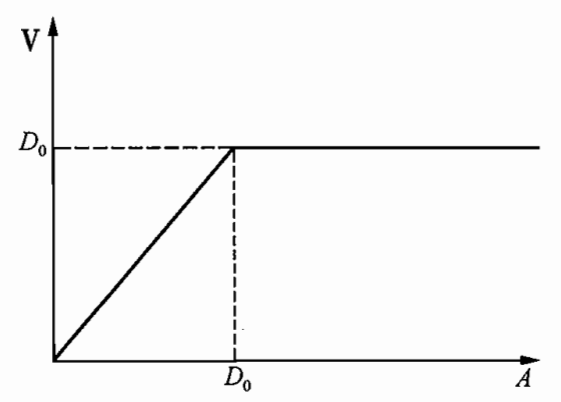
    投资学知识点

    • 债务的价值V_D相当于行权价值为D，当前股价为A的看跌期权，加上终值为D的现金
    • V_D=\frac{D}{(1+r_f)^n}-P
      债权人拥有一个终值为D的债权
      债权人向股东出售了一个看跌期权
    • V_E=A-V_D
      股东拥有公司
      股东欠债权人一个终值为D的债权
      股东从债权人购买了一个看跌期权
  3. 由于权益和债务都可以视作期权，因此可以用二叉树定价

期权的数学描述

  1. 随机过程
    \begin{align} &\frac{\mathrm d S_t}{S_t}=r\mathrm d t +\sigma \mathrm d W_t\quad\quad \mathrm d W_t\sim \mathrm N(0,t) \\ &\frac{S_{\Delta t}-S_0}{S_0}=r \Delta t +\sigma \epsilon\sqrt{ \Delta t} \quad\quad\epsilon \sim \mathrm{N}(0,1) \end{align}

    • r,\sigma都是年化的，\Delta t是占一年的百分比
  2. 服从分布
    \begin{align} &\frac{S_t}{S_0}\sim e^{\mathrm {N}\left[\left(r-\frac{\sigma^2}{2}\right)t,\sigma^2t\right]} \\ &\frac{S_{\Delta t}}{S_0}\sim 1+\mathrm{N}(r\Delta t,\sigma^2\Delta t) \end{align}

    • r,\sigma都是年化的，\Delta t是占一年的百分比
    • 当t\rightarrow 0， e^{\mathrm {N}\left[\left(r-\frac{\sigma^2}{2}\right)t,\sigma^2t\right]}\sim 1+\mathrm{N}(r t,\sigma^2 t)

均值方差模型

CAL

  1. 定义
    • 投资者在无风险资产与风险资产之间构建投资组合，组合收益率与总风险的关系
  2. 公式
    • CAL的表达式
      \begin{align} \because\quad&\begin{cases} &w_1+w_f=1\\ &r_p=w_1r_1+w_fr_f\\ &\sigma_p=w_1\sigma_1 \end{cases} \\\\ \therefore\quad&r_p=r_1+\frac{r_f-r_1}{\sigma_1}\sigma_p \end{align}
    • 最优头寸
      \begin{align} \because\quad&U=r-\frac{1}{2}A\sigma^2 \\ &\frac{\mathrm dr_p}{\mathrm{d \sigma_p}}=\frac{\mathrm dU}{\mathrm{d \sigma_p}} \\ \therefore\quad&\frac{r_f-r_1}{\sigma_1}=-A\sigma_p \\ \therefore\quad&w_1=\frac{r_1-r_f}{A\sigma_1^2} \end{align}

CML

  1. 定义
    • 斜率（即夏普比率）最大的CAL，对应的风险资产记为市场组合M
  2. 两风险资产下的CML
    • 有效边界
      \begin{aligned} \because\quad&\begin{cases} &w_1+w_2=1\\ &r_p=w_1r_1+w_2r_2\\ &\sigma_p^2=w_1^2\sigma_1^2+w_2^2\sigma_2^2+2w_1w_2\sigma_1\sigma_2\rho \end{cases} \\\\ \therefore\quad&\sigma_p^2(r_1-r_2)^2=Ar_p^2-2Br_p+C \\ &A=\sigma_1^2+\sigma_2^2-2\sigma_1\sigma_2\rho=\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} \sigma_1 \\ \sigma_2\\\end{pmatrix} \\ &B=\sigma_1^2r_2+\sigma_2^2r_1-\sigma_1\sigma_2\rho (r_1+r_2)=\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} r_2& \\ & r_1\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} \sigma_1\\ \sigma_2\\\end{pmatrix} \\ &C=\sigma_1^2r_2^2+\sigma_2^2r_1^2-2\sigma_1\sigma_2\rho r_1 r_2=\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} r_2& \\ & r_1\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} r_2& \\ & r_1\\\end{pmatrix}\begin{pmatrix} \sigma_1\\ \sigma_2\\\end{pmatrix} \end{aligned}
    • 最小方差组合MVP
      \begin{align} \because\quad&\frac{\mathrm{d } \sigma_p}{\mathrm{d}r_p }=\frac{Ar_p-B}{\sigma_p(r_1-r_2)^2}=0 \\ \therefore\quad&r_p=\frac{B}{A}=\frac{\sigma_1^2r_2+\sigma_2^2r_1-\sigma_1\sigma_2\rho (r_1+r_2)}{\sigma_1^2+\sigma_2^2-2\sigma_1\sigma_2\rho}=\frac{\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} r_2& \\ & r_1\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} \sigma_1\\ \sigma_2\\\end{pmatrix}}{\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} \sigma_1 \\ \sigma_2\\\end{pmatrix}} \\ &\sigma_p^2=\frac{\sigma_1^2\sigma_2^2(1-\rho^2)}{\sigma_1^2+\sigma_2^2-2\sigma_1\sigma_2\rho}=\frac{|\Sigma|}{\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} \sigma_1 \\ \sigma_2\\\end{pmatrix}} \\ \therefore\quad&w_1=\frac{r_p-r_2}{r_1-r_2}=\frac{\sigma_2^2-\sigma_1\sigma_2\rho}{\sigma_1^2+\sigma_2^2-2\sigma_1\sigma_2\rho}= \frac{\begin{pmatrix} 0 & \sigma_2\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} \sigma_1 \\ \sigma_2\\\end{pmatrix}}{\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} \sigma_1 \\ \sigma_2\\\end{pmatrix}}=\frac{\langle\bar{\sigma_1}|\rho|\sigma\rangle}{\langle\sigma|\rho|\sigma\rangle} \\ &w_2=\frac{r_1-r_p}{r_1-r_2}=\frac{\sigma_1^2-\sigma_1\sigma_2\rho}{\sigma_1^2+\sigma_2^2-2\sigma_1\sigma_2\rho}=\frac{\begin{pmatrix} \sigma_1 & 0\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} \sigma_1 \\ \sigma_2\\\end{pmatrix}}{\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} \sigma_1 \\ \sigma_2\\\end{pmatrix}}=\frac{\langle\bar{\sigma_2}|\rho|\sigma\rangle}{\langle\sigma|\rho|\sigma\rangle} \\ \text{其中}\quad&\text{协方差矩阵}\Sigma=\begin{pmatrix}\sigma_1^2&\sigma_1\sigma_2\rho\\\sigma_1\sigma_2\rho&\sigma_2^2\end{pmatrix} \end{align}
    • 市场组合
      \begin{align} \because\quad&\frac{\mathrm{d}r_p }{\mathrm{d } \sigma_p}=\frac{\sigma_p(r_1-r_2)^2}{Ar_p-B}=\frac{r_p-r_f}{\sigma_p} \\ \therefore\quad&r_p=\frac{Br_f-C}{Ar_f-B}=\frac{\sigma_1^2r_2r_2^\ast+\sigma_2^2r_1r_1^\ast-\sigma_1\sigma_2\rho (r_2r_1^\ast+r_1r_2^\ast)}{\sigma_1^2r_2^\ast+\sigma_2^2r_1^\ast-\sigma_1\sigma_2\rho (r_2^\ast+r_1^\ast)}=\frac{\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} r_2& \\ & r_1\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} r_2^\ast& \\ & r_1^\ast\\\end{pmatrix}\begin{pmatrix} \sigma_1\\ \sigma_2\\\end{pmatrix}}{\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} r_2^\ast& \\ & r_1^\ast\\\end{pmatrix}\begin{pmatrix} \sigma_1\\ \sigma_2\\\end{pmatrix}} \\ &\sigma_p^2=\frac{\sigma_1^2\sigma_2^2(1-\rho^2)(\sigma_2^2r_1^{\ast 2}+\sigma_1^2r_2^{\ast 2}-2\sigma_1\sigma_2\rho r_1^\ast r_2^\ast)}{\left[\sigma_1^2r_2^\ast+\sigma_2^2r_1^\ast-\sigma_1\sigma_2\rho(r_1^\ast+r_2^\ast)\right]^2}=\frac{|\Sigma|\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} r_2^\ast& \\ & r_1^\ast\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} r_2^\ast& \\ & r_1^\ast\\\end{pmatrix}\begin{pmatrix} \sigma_1\\ \sigma_2\\\end{pmatrix}}{\left[\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} r_2^\ast& \\ & r_1^\ast\\\end{pmatrix}\begin{pmatrix} \sigma_1\\ \sigma_2\\\end{pmatrix}\right]^2} \\ \therefore\quad&w_1=\frac{r_p-r_2}{r_1-r_2}=\frac{\sigma_2^2r_1^\ast-\sigma_1\sigma_2\rho r_2^\ast}{\sigma_1^2r_2^\ast+\sigma_2^2r_1^\ast-\sigma_1\sigma_2\rho(r_1^\ast+r_2^\ast)}=\frac{\begin{pmatrix} 0 & \sigma_2\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} r_2^\ast& \\ & r_1^\ast\\\end{pmatrix}\begin{pmatrix} \sigma_1\\ \sigma_2\\\end{pmatrix}}{\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} r_2^\ast& \\ & r_1^\ast\\\end{pmatrix}\begin{pmatrix} \sigma_1\\ \sigma_2\\\end{pmatrix}}=\frac{\langle\bar{\sigma_1}|\rho|r^\ast|\sigma\rangle}{\langle\sigma|\rho|r^\ast|\sigma\rangle} \\ &w_2=\frac{r_1-r_p}{r_1-r_2}=\frac{\sigma_1^2r_2^\ast-\sigma_1\sigma_2\rho r_1^\ast}{\sigma_1^2r_2^\ast+\sigma_2^2r_1^\ast-\sigma_1\sigma_2\rho(r_1^\ast+r_2^\ast)}=\frac{\begin{pmatrix} \sigma_1& 0 \\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} r_2^\ast& \\ & r_1^\ast\\\end{pmatrix}\begin{pmatrix} \sigma_1\\ \sigma_2\\\end{pmatrix}}{\begin{pmatrix} \sigma_1 & \sigma_2\\\end{pmatrix}\begin{pmatrix} 1& -\rho\\-\rho & 1\\\end{pmatrix}\begin{pmatrix} r_2^\ast& \\ & r_1^\ast\\\end{pmatrix}\begin{pmatrix} \sigma_1\\ \sigma_2\\\end{pmatrix}}=\frac{\langle\bar{\sigma_2}|\rho|r^\ast|\sigma\rangle}{\langle\sigma|\rho|r^\ast|\sigma\rangle} \\ \text{其中}\quad&r_1^\ast=r_1-r_f,\ r_2^\ast=r_2-r_f \end{align}
    • 最优头寸
      \begin{align} &w_1=\frac{r_p-r_f}{A\sigma_p^2}\cdot\frac{r_p-r_2}{r_1-r_2} \\ &w_2=\frac{r_p-r_f}{A\sigma_p^2}\cdot\frac{r_1-r_p}{r_1-r_2} \\ &w_f=1-\frac{r_p-r_f}{A\sigma_p^2} \end{align}
  3. 特殊情形
    • 不允许借: 可行域为无风险切线 → M → 有效前沿
    • 不允许贷: 可行域为有效前沿 → M → 无风险切线
    • 不允许借贷: 可行域为有效前沿
    • 借款利率更大: 可行域为无风险切线 → M → 有效前沿 → 借款切点 → 借款切线
      在无风险切线 → M上存在贷，收益率为无风险利率
      在M → 有效前沿 → 借款切点上不借也不贷
      在借款切点 → 借款切线上存在借，借款利率大于无风险利率
    • 风险极其厌恶: 只有角点解，只投资无风险资产

CAPM

  1. 公式
    r_p=r_f+\beta_p(r_m-r_f)+e_p\quad\quad e_p\sim\mathrm N(0,\sigma^2_{e,p})
  2. 性质
    • 总风险：\sigma^2_p=\mathrm D(r_p)=\beta^2_p\sigma^2_m+\sigma^2_{e,p}，其中\beta^2_p\sigma^2_m为系统性风险，\sigma^2_{e,p}为非系统性风险

VaR

  1. 定义
    • \mathrm P(\Delta V\le - \operatorname{VaR})=1-\alpha
    • r为算术平均收益率，则损益为正态分布
      \begin{aligned} & \operatorname{VaR_\%}(\alpha)=-\left(\mu_r-z_\alpha \times \sigma_r\right) \\ & \operatorname{VaR_\$}(\alpha)=-\left(\mu_r-z_\alpha \times \sigma_r\right) \times P_{t-1} \\ & \operatorname{VaR_\$}(\alpha)=-\left(\mu_{P / L}-z_\alpha \times \sigma_{P / L}\right) \end{aligned}
    • R为几何平均收益率，则损益为对数正态分布
      \begin{aligned} & \operatorname{VaR_\%}(\alpha)=\left(1-e^{\mu_R-z_\alpha \times \sigma_R}\right) \\ & \operatorname{VaR_\$}(\alpha)=\left(1-e^{\mu_R-z_\alpha \times \sigma_R}\right) \times P_{t-1} \end{aligned}
  2. 天数转换
    \frac{\mu_t}{t}=\frac{\mu_T}{T}\quad \frac{\sigma_t}{\sqrt t}=\frac{\sigma_T}{\sqrt T}
  3. 分位表
    • z_{1\%}=2.33
    • z_{2.5\%}=1.96
    • z_{5\%}=1.65
    • z_{10\%}=1.28

发表评论 取消回复
表情 图片 链接 代码

分享