公司理财知识点

金专>金融学
realhuhu 534 0

简写表

利润表项目

  1. S：(净)营业收入
  2. COGS：产品销售成本
  3. GI：毛利润，GI=S-COGS
  4. SG\&A：销售、行政及管理费用
  5. EBITDA：息税折旧摊销前利润，EBITDA=GI-SG\&A(\pm \text{other taxable items})
  6. D：折旧
    • D\&A：折旧和摊销
  7. EBIT：息税前利润，EBIT=EBITDA-D\&A
  8. I：利息费用
  9. EBT：税基，EBT=EBIT-I
  10. T：所得税支出，包括当期所得税和递延所得税
    • CT：当期所得税
    • DT：递延所得税
  11. NI：净利润，NI=EBT-T(\pm \text{other nontaxable items})
    • RE：留存收益
    • Div：股利（包括普通股与优先股）

资产负债表项目

  1. A：资产
    • CA：流动资产，包括现金及其等价物、应收账款、预付账款和存货
      CCE：现金及其等价物
      AR：应收账款
      PE：预付账款
      Inv：存货
    • FA：固定资产，包括地产、厂房及设备和无形资产
      PP\&E：地产、厂房及设备
      AD：累计折旧
      IA：无形资产
      AA：累计摊销
  2. L：负债
    • CL：流动负债，包括应付账款和预收账款
      AP：应付账款
      UR：预收账款
    • LTL：长期负债，包括递延税款和长期债务
      DTL：递延税款
      LTD：长期债务
  3. E：所有者权益
    • ARE：累积留存收益

现金流分析

财务现金流

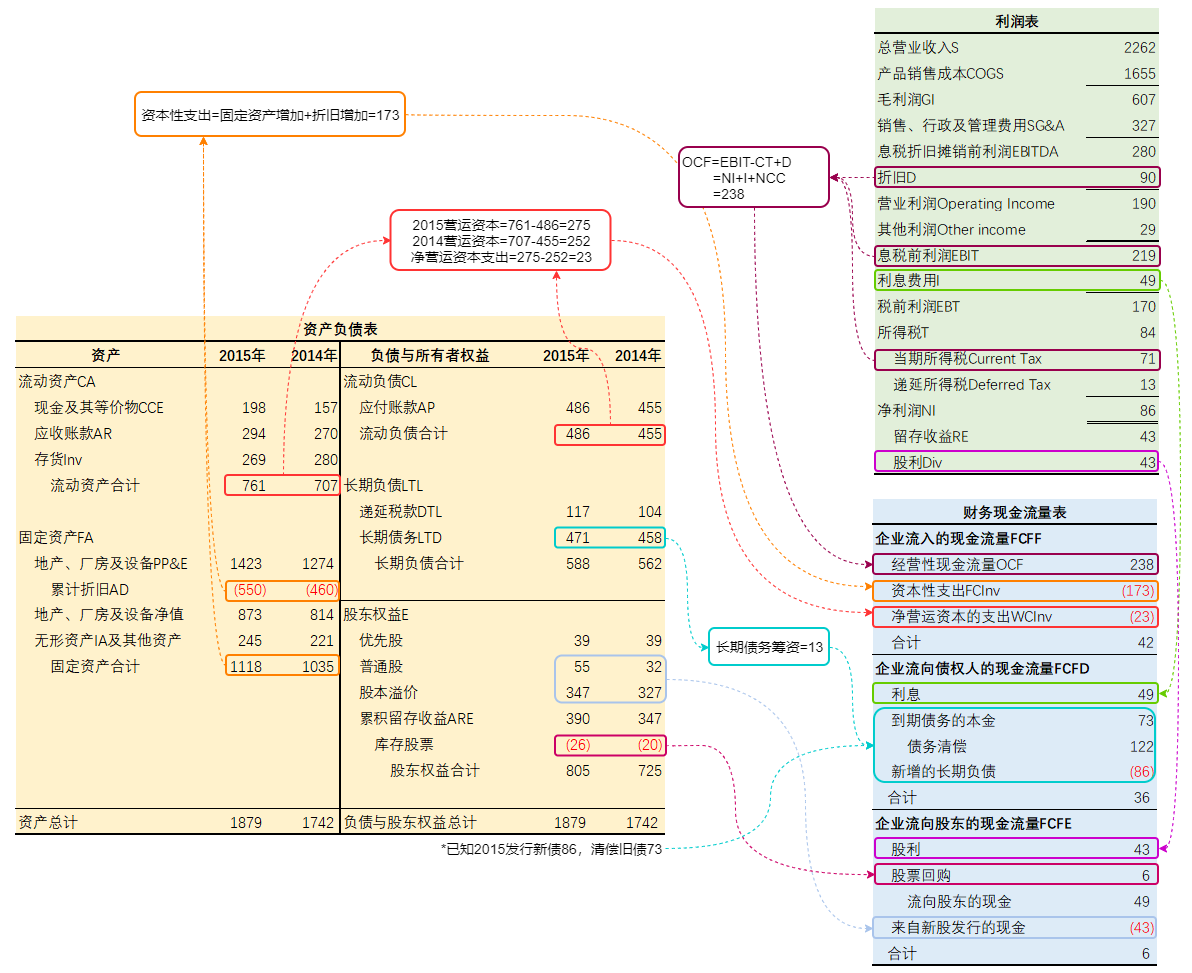
公司理财知识点

  1. 自由现金流FCFF：企业在所有活动中获得的现金流入，又叫资产现金流，为负说明股东债权人的钱流向资产，也叫CF(A)
    FCFF = OCF - FCInv - WC Inv = NI + I + DT + \Delta CL -\Delta A

    • 经营性现金流OCF：企业在经营活动中获得的现金流入
      OCF = NI + I + NCC = NI + I + D\&A + DT
    • 资本性支出FCInv：固定资产原值（剔除了折旧摊销）的增加额
      FCInv = \Delta FA +\Delta AD + \Delta AA = \Delta FA + D\&A
      包括固定资产下除折旧摊销以外的科目，既包括有形资产，也包括无形资产
      折旧摊销在OCF中考虑，不在FCInv中体现
    • 净营运资本支出WCInv: 净营运资本的增加额
      WCInv = \Delta CA - \Delta CL
      包括了流动资产和流动负债科目
    • 可以理解为从NI开始调整得到FCFF
      I为利息，在FCFD中再支付给债权人，因此为加项
      DT为递延税款，该现金流尚未实现，因此计算真实现金流时需要加回来
      \Delta CL为流动负债，该现金流尚未实现，因此计算真实现金流时需要加回来
      \Delta A为净资产的增加，消耗了真实现金流，因此为减项
  2. 流向债权人的现金流FCFD： 企业支付给债权人的现金流，也叫CF(B)
    FCFD = I - \Delta LTD

    • 利息支付和长期债务的减少表示现金流向债权人
    • 剔除了长期负债中的递延税款，递延税款在FCFF的OCF中考虑
  3. 流向股东的现金流FCFE：企业支付给股东的现金流，也叫CF(S)
    \begin{align} FCFE&=FCFF-FCFD=NI+\Delta L-\Delta A=NI-\Delta E \\ &=NI-\Delta\text{普通股、优先股、股本溢价}-\Delta ARE+\Delta{库存股} \\ &=NI-RE-\text{新股发行}+\text{股票回购} \\ &=Div-\text{新股发行}+\text{股票回购} \end{align}

    • 库存股为备抵科目，因此要变号
    • 股利支付、股票回购表示现金流向股东，新股发行表示现金流向公司

单纯计算OCF时用税前利息I（罗斯教材），项目估值时用税后利息I(1-t)（博迪教材)
因为FCFF是站在公司角度的一次分配的现金流，所以税为EBIT\times t而不是(EBIT-I)\times t
对于FCFD，税盾价值由国家支付，真正由企业支付的利息为I(1-t)，因此也要替换

会计现金流

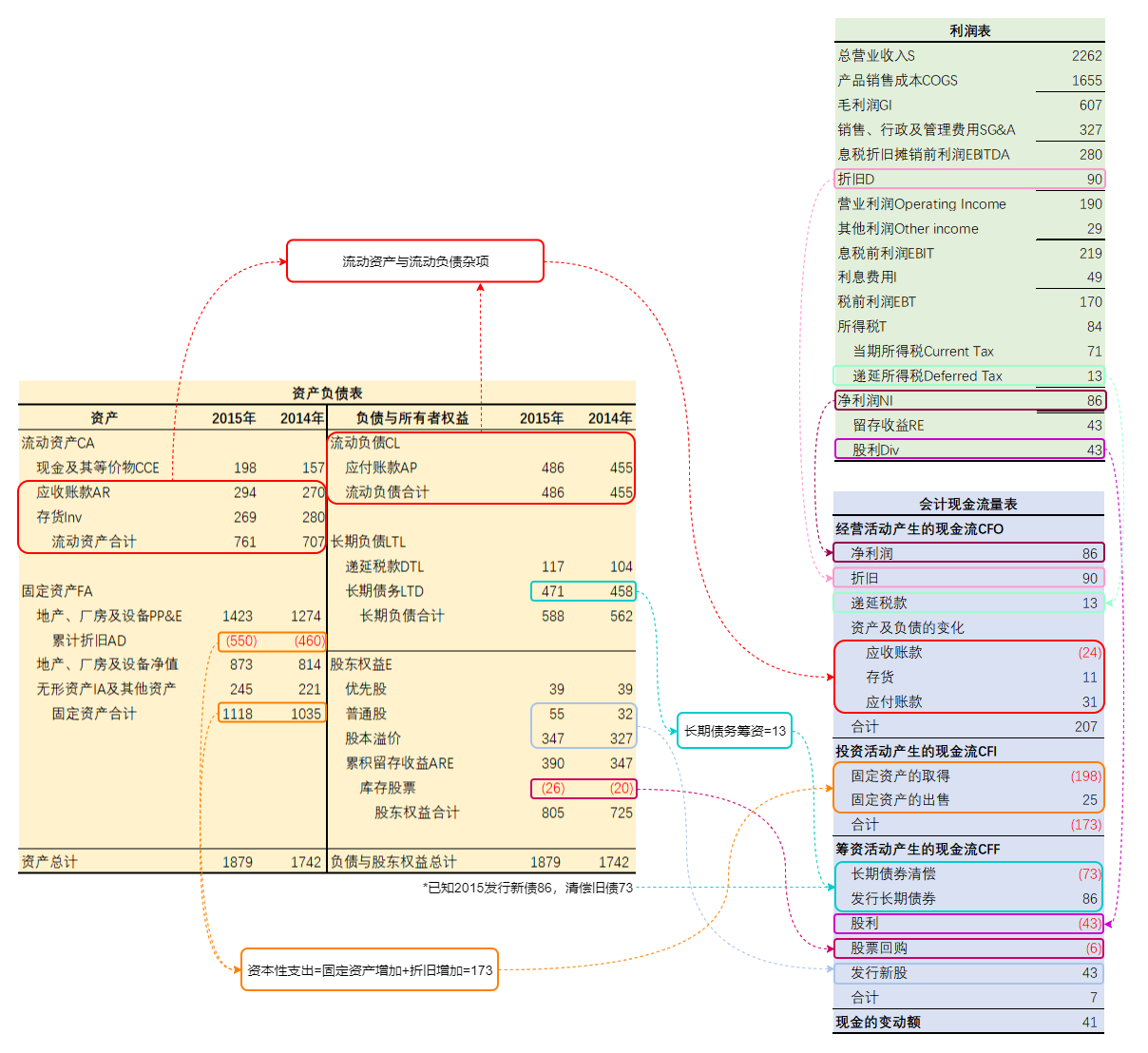
公司理财知识点

  1. 经营活动产生的现金流CFO：企业日常经营活动中产生的现金流
    CFO = NI + NCC - NRI - \Delta (CA-CCE) + \Delta CL

    • 由净利润调整而来，加上非付现成本、减去非经常性项目NRI，再考虑除现金以外的流动资产和流动负债的变动
  2. 投资活动产生的现金流CFI：企业买卖长期资产、交易非交易性证券和借钱或收回借出的本金
    CFI=NRI -\Delta FA - D\&A=NRI-FCInv

    • 对应固定资产（简化处理）
  3. 筹资活动产生的现金流CFF：企业融资活动产生的现金流
    CFF = \Delta LTD - Div + \text{新股发行} - \text{股票回购} = I-FCFF

    • 对应长期负债和所有者权益

财务指标

报表标准化

  1. 实现不同公司之间、不同时期之间的报表比较
  2. 资产负债表：同除以总资产，表示为总资产的百分比
  3. 利润表：同除以销售额，表示各部分占了多少销售额

偿债指标

短期偿债能力指标/流动性指标

  1. 流动比率：表示流动资产对流动负债的保障倍数，低于1则净营运资本为负
    \text{流动比率}=\frac{CA}{CL}=\frac{CCE+AR+PE+Inv}{CL}
  2. 速动比率：存货与预付账款变现与能力低，因此排除在外
    \text{速动比率}=\frac{CCE+AR}{CL}
  3. 现金比率：只考虑现金对流动负债的保障程度，是短期债权人最关注现金比率
    \text{现金比率}=\frac{CCE}{CL}

长期偿债能力指标/杠杆比率

  1. 总负债比率：资产中有多少是负债带来的
    \text{总负债比率}=\frac{L}{A}
  2. 负债权益比：股东权益对负债的放大倍数
    \text{负债权益比}=\frac{L}{E}
  3. 权益乘数：股东权益对资产的放大倍数
    \text{权益乘数}=\frac{A}{E}=1+\text{负债权益比}
  4. 利息倍数：衡量公司负担利息的能力
    \text{利息倍数}=\frac{EBIT}{I}
  5. 现金对利息的保障倍数：加回了非现金项目，更符合实际
    \text{现金对利息的保障倍数}=\frac{EBITDA}{I}

周转指标

  1. 存货
    • 周转率\frac{COGS}{\overline{Inv}}：仓库一年周转多少次存货，越高越好
    • 周转天数DOH=\frac{365\times \overline{Inv}}{COGS}：平均需要多久才能变现存货，越低越好
  2. 应收账款
    • 周转率\frac{S(最好是赊销收入)}{\overline{AR}}：一年完成多少次应收账款的收回，越高越好
    • 周转天数DSO=\frac{365\times \overline{AR}}{S}：平均多久收回赊销货款，或者还有多长时间的赊销货款未收回，越低越好
  3. 应付账款
    • 周转率\frac{P(最好是赊购支出)}{\overline{AP}}：一年完成多少次应付账款的支付，越低越好
    • 周转天数DPO=\frac{365\times \overline{AP}}{P}：平均多久支付赊购货款，或者还有多长时间的赊购货款未支付，越高越好
  4. 总资产、固定资产、营运资本
    • 周转率\frac{S}{\overline{A}}：每一元的总资产、固定资产、营运资本产生了多少元收入，越高越好
    • 周转天数DPO=\frac{365\times \overline{A}}{S}：每一元的总资产、固定资产、营运资本平均需要多久才能收回，越低越好
  5. 周期
    • 经营周期OC=DOH+DSO=DPO+CCC
    • 现金周期CCC=DOH+DSO-DPO

盈利指标

  1. 销售利润率ROS
    ROS=\frac{NI}{S}

    • 利润表标准化后的净利润项目
    • 从1单位的销售额中获取了多少利润
  2. EBITDA利润率
    \text{EBITDA利润率}=\frac{EBITDA}{S}

    • 利润表标准化后的EBITDA项目
    • 从1单位的销售额中获取了多少EBITDA
    • 加回了非现金项目，不受资本结构和税的影响
  3. 资产收益率ROA
    ROA=\frac{NI}{A}
  4. 权益收益率/净资产收益率ROE
    ROE=\frac{NI}{E}=\frac{(EBIT-D\times r_d)\times(1-t)}{E}

    • 当\frac{EBIT}{E+D}\gt r_d时，提高负债可以增加ROE
      \frac{\mathrm dROE}{\mathrm dD}=\frac{1-t}{E}\times\left(\frac{EBIT}{D+E}-r_d\right)

价值指标

  1. 市盈率P/E
    P/E=\frac{CAP}{NI}=\frac{P}{EPS}=\frac{D}{(r-g)\times EPS}

    • 历史市盈率: \frac{P_0}{EPS_0}，预期市盈率: \frac{P_0}{EPS_1}
    • 股票的价格是股票收益的多少倍，即投资者愿意为每股利润支付多少倍的钱
    • 高市盈率可能表示投资者看好公司的前景，也可能是公司利润太低
  2. 市净率P/B
    PB=\frac{CAP}{E}=\frac{P}{BPS}=\frac{D}{(r-g)\times BPS}

    • E为扣除清算价值等抵扣项目后的净值
  3. 市值账面比M/B
    M/B=\frac{CAP}{E}=\frac{P}{BPS}

    • 账面价值为投入的成本，市值为当前的价值，大于1表示为股东创造了价值
  4. 企业价值乘数
    \text{企业价值乘数}=\frac{EV}{EBITDA}

    • 企业价值EV：股票市值 + 附息债券市场价值 - 现金
    • 由市盈率调整而来，不考虑非现金项目、资本结构等，因此可以用于比较不同公司

其它

  1. 杜邦恒等式
    \begin{align} ROE=&\frac{NI}{E} \\ =&\frac{NI}{A}\frac{A}{E}=ROA\times\text{权益乘数} \\ =&\frac{NI}{S}\frac{S}{A}\frac{A}{E}=ROS\times\text{总资产周转率}\times\text{权益乘数} \end{align}

    • ROE受经营效率、资产运用效率、财务杠杆的影响
    • 权益乘数与ROA,ROS负相关
  2. 外部融资需要量EFN
    EFN=\text{自然增长的资产}\times\text{销售额增长率}-\text{自然增长的负债}\times\text{销售额增长率}-\text{预计销售额}\times ROS \times b

    • 由于销售额增长时，资产等比例增加，负债只有自然增长的负债等比例增加，为了使资产负债表平衡，需要外部融资
    • 第三项即为留存收益，随着销售额增加而增加，但并非等比例增加
    • EFN的融资方式包括短期借款、长期借款、权益融资等
    • 由于留存收益会影响权益数值，若销售额增长率较小，EFN为负数，出现资金冗余
  3. 内部增长率
    g=ROA_0\times b=\frac{ROA\times b}{1- ROA\times b}

    • 假设资产都是自然增长、负债都不自然增长、不进行外部融资时，使得EFN为0的销售额增长率。此时财务杠杆下降
    • ROA_0为期末净利润/期初资产，ROA_1为期末净利润/期末资产，此时有A_1=A_0+NI\times b=A_0(1+g)
  4. 可持续增长率
    g=ROE_0\times b=\frac{ROE_1\times b}{1- ROE_1\times b}

    • 假设资产都是自然增长、负债都不自然增长、只通过债务外部融资，使得EFN与预期留存收益之比等于负债权益比的销售额增长率。此时财务杠杆不变
    • ROE_0为期末净利润/期初权益，ROE_1为期末净利润/期末权益，此时有E_1=E_0+NI\times b=E_0(1+g)
    • 不改变经营效率和财务政策的前提下，可持续增长率等于实际增长率
    • 由此可见，公司可持续增长率受ROE三因素和留存收益率b的影响

MM定理

无税MM定理

  1. 前提假设
    • 公司价值V等于债务价值B加上股票价值S
    • 无负债公司与负债公司有相同的EBIT且无增长
    • 债务资本成本r_b保持不变，等价于债务无风险，且等于借贷利率
  2. 命题一
    V_L=V_U

    • 证明
      组合一购入占U公司总股票的\alpha比例的股票，持有一年后卖出，持有期收益Y_U包括股息与资本利得
      Y_U=\alpha EBIT
      组合二购入占L公司总股票的\alpha比例的股票、占L公司总债券的\alpha比例的债券，持有一年后卖出，则持有期收益Y_L为
      Y_L=\alpha (EBIT-B_L r_b)+\alpha B_L r_b=\alpha EBIT
      两个组合收益相同，因此期初投资相同
      \alpha S_U=\alpha B_L+\alpha S_L\quad\Rightarrow\quad S_U=B_L+S_L
      由假设可知V_L=V_U
  3. 命题二
    r_s=r_0+\frac{B}{S}(r_0-r_b)

    • 证明
      持有期为一年，无负债公司股票的要求回报率为r_0，有负债公司股票的要求回报率为r_s，即
      \begin{align} \because\quad&r_0=\frac{\alpha EBIT}{\alpha S_U} \\ &r_s=\frac{\alpha (EBIT-B_L r_b)}{\alpha S_L} \\ \therefore\quad&S_Lr_s=S_Ur_0-B_L r_b \end{align}
      根据命题一，代入S_U=B_L+S_L，得到r_s=r_0+\frac{B_L}{S_L}(r_0-r_b)
    • 根据r_b,r_s求r_0
      r_0=\frac{r_s+\frac{B}{S}r_b}{1+\frac{B}{S}}
  4. 推论一：有负债公司的加权资本成本
    r_{WACC}=\frac{S}{B+S}r_s+\frac{B}{B+S}r_b

    • 证明
      \begin{align} \because\quad&V_L=V_U \\ &V_L=\frac{EBIT}{r_{WACC}} \\ &V_U=\frac{EBIT}{r_0} \\ \therefore\quad&r_{WACC}=r_0 \end{align}
      由命题二解得r_{WACC}=\frac{S_L}{B_L+S_L}r_s+\frac{B_L}{B_L+S_L}r_b
    • 表明无税收时，有负债公司的加权资本成本就是无负债公司的股票资本成本
  5. 推论二：有负债公司的\beta_s
    \beta_s=\beta_0\left(1+\frac{B}{S}\right)

    • 证明
      \begin{align} \because\quad& r_s=r_0+\frac{B}{S}(r_0-r_b) \\ \therefore\quad& r_f+\beta_s(r_m-r_f)=r_f+\beta_0(r_m-r_f)+\frac{B}{S}[r_f+\beta_0(r_m-r_f)-r_f] \\ &\beta_s=\beta_0\left(1+\frac{B}{S}\right) \end{align}
      必须满足r_b=r_f的前提条件才能使用
    • 若负债有\beta，则
      \beta_s=\beta_0+\frac{B}{S}(\beta_0-\beta_b)
      类似命题二

有税MM定理

  1. 前提假设
    • 公司价值V等于债务价值B加上股票价值S
    • 无负债公司与负债公司有相同的EBIT且无增长
    • 债务资本成本r_b保持不变，等价于债务无风险，且等于借贷利率
    • 公司税、权益个人所得税、债务个人所得税分别为t,t_s,t_b
  2. 命题一
    V_L=V_U+\left[1-\frac{(1-t)(1-t_s)}{1-t_b}\right]B

    • 证明
      组合一购入占U公司总股票的\alpha比例的股票，持有一年后卖出，持有期收益Y_U包括股息与资本利得
      Y_U=\alpha EBIT(1-t)(1-t_s)
      组合二购入占L公司总股票的\alpha比例的股票、占L公司总债券的\alpha\frac{(1-t)(1-t_s)}{1-t_b}比例的债券，持有一年后卖出，则持有期收益Y_L为
      Y_L=\alpha (EBIT-B_L r_b)(1-t)(1-t_s)+\alpha\frac{(1-t)(1-t_s)}{1-t_b} B_L r_b(1-t_b)=\alpha EBIT(1-t)(1-t_s)
      两个组合收益相同，因此期初投资相同
      \alpha S_U=\alpha\frac{(1-t)(1-t_s)}{1-t_b} B_L+\alpha S_L\quad\Rightarrow\quad S_U=B_L+S_L+\left[\frac{(1-t)(1-t_s)}{1-t_b} -1\right]B_L
      由假设可知V_L=V_U+\left[1-\frac{(1-t)(1-t_s)}{1-t_b}\right]B_L
    • 若满足t_s=t_b，可化简为
      V_L=V_U+tB
  3. 命题二
    r_s=r_0+\frac{B}{S}(r_0-r_b)(1-t)(1-t_s)

    • 证明
      持有期为一年，无负债公司股票的要求回报率为r_0，有负债公司股票的要求回报率为r_s，即
      \begin{align} \because\quad&r_0=\frac{\alpha EBIT(1-t)(1-t_s)}{\alpha S_U} \\ &r_s=\frac{\alpha (EBIT-B_L r_b)(1-t)(1-t_s)}{\alpha S_L} \\ \therefore\quad&S_Lr_s=S_Ur_0-B_L r_b(1-t)(1-t_s) \end{align}
      根据命题一，代入S_U=B_L+S_L，得到r_s=r_0+\frac{B_L}{S_L}(r_0-r_b)(1-t)(1-t_s)
    • 根据r_b,r_s求r_0
      r_0=\frac{r_s+\frac{B}{S}(1-t)(1-t_s)r_b}{1+\frac{B}{S}(1-t)(1-t_s)}
    • 若满足t_s=0
      \begin{align} &r_s=r_0+\frac{B}{S}(r_0-r_b)(1-t) \\ &r_0=\frac{r_s+\frac{B}{S}(1-t)r_b}{1+\frac{B}{S}(1-t)} \end{align}
  4. 推论一：有负债公司的加权资本成本
    \begin{align} &r_{WACC}=\frac{S}{B+S}r_sX+\frac{B}{B+S}r_b(1-t)[(1-t_s)X+t_s-t_b] \\ &X=\frac{1-t_b\frac{1}{1+\frac{B}{S}(1-t)(1-t_s)}}{1-t_b} \end{align}

    • 证明
      \begin{align} \because\quad&V_L=V_U+\left[1-\frac{(1-t)(1-t_s)}{1-t_b}\right]B \\ &V_U=\frac{EBIT(1-t)(1-t_s)}{r_0} \\ &V_L=\frac{(EBIT-I)(1-t)(1-t_s)+I(1-t)(1-t_d)}{r_{WACC}}=B+S \end{align}
      解得r_{WACC}
    • 若t_b=0
      r_{WACC}=\frac{S}{B+S}r_s+\frac{B}{B+S}r_b(1-t)
    • 若t_b=t_s=0
      r_{WACC}=r_0\left(1-\frac{B}{B+S}t\right)
  5. 推论二：有负债公司的\beta_s
    \beta_s=\beta_0\left[1+\frac{B}{S}(1-t)(1-t_s)\right]

    • 证明
      \begin{align} \because\quad& r_s=r_0+\frac{B}{S}(r_0-r_b)(1-t)(1-t_s) \\ \therefore\quad& r_f+\beta_s(r_m-r_f)=r_f+\beta_0(r_m-r_f)+\frac{B}{S}(1-t)(1-t_s)[r_f+\beta_0(r_m-r_f)-r_f] \\ &\beta_s=\beta_0\left[1+\frac{B}{S}(1-t)(1-t_s)\right] \end{align}
      必须满足r_b\equiv r_f的前提条件才成立
    • 若负债有\beta，则
      \beta_s=\beta_0+\frac{B}{S}(\beta_0-\beta_b)(1-t)(1-t_s)
      类似命题二

增长现金流

  1. 固定债务
    • 此时有税MM定理仍成立
  2. 固定杠杆
    • 当现金流增长时，债务存在风险，公司的税盾不再是tB
      V_L=V_U+tB\quad\Rightarrow\quad V_L=V_U^\ast+\sum \mathrm{PV}(\text{税盾})
      ME定理：假设公司在某些固定时间点将杠杆调整为期初值，在两次调整之间任由杠杆变动，则税盾从发生时间折现到上一个调整时间点时用r_b折现，在时间点之间这些时用r_0折现，据此求得\sum\mathrm{PV}(\text{税盾})
    • 当现金流增长时，税盾不确定，不能降低股权资本成本
      r_s=r_0+\frac{B}{S}(r_0- r_b)(1-t)\quad\Rightarrow\quad r_s=r_0+\frac{B}{S}(r_0-r_b)
      此时r_0=WACC=\frac{S}{B+S}r_s+\frac{B}{B+S}r_b
  3. 一般情况下的r_{WACC}
    r_{WACC}=r_0-\frac{B}{B+S}t\left[r_d+\frac{T^\ast}{tB}(r_0-r_d)\right]\quad\quad T^\ast\text{为由固定债务产生的税盾}

    • 固定杠杆时，由于持续调整债务，因此T^\ast=0，此时
      r_{WACC}=r_0-\frac{B}{B+S}tr_b
    • 固定债务时，债务恒定，因此T^\ast=tB，此时
      r_{WACC}=r_0-\frac{B}{B+S}tr_0
      就是有税MM定理二的中的推论

公司估值

现金流

  1. 流向公司的现金流FCFF
    FCFF=EBIT(1-t)+D-FCInv-WCInv

    • 就是将财务现金流中FCFF的I换成I(1-t)
    • 展开得到
      FCFF=EBIT(1-t)-\Delta LTL-\Delta E
      据此可以计算非永续项目的FCFF，一般来说利润全部作为股利发放且期间无股权融资，因此\Delta E=0
    • 这表明投资策略不变时，债务融资规模不会影响FCFF
  2. 流向债权人的现金流FCFD
    FCFD=I(1-t)-\Delta LTD

    • 就是将财务现金流中FCFD的I换成I(1-t)
  3. 流向股东的现金流FCFE
    FCFE=FCFF-FCFD=NI-\Delta E=Div-\text{新股发行}+\text{股票回购}
  4. 无杠杆现金流UCF
    UCF=EBIT(1-t)

    • 满足一定假设条件下的FCFF
      业务处于稳定期，即折旧和投资可以抵消
      营运资本滚动投入，即净营运资本始终为零
  5. 杠杆现金流LCF
    UCF=(EBIT-I)(1-t)

    • 满足一定假设条件下的FCFE
      业务处于稳定期，即折旧和投资可以抵消
      营运资本滚动投入，即净营运资本始终为零
      资本结构保持稳定，即新股发行与股票回购抵消、净利润全部作为股利

估值方法

  1. WACC法：直接站在公司角度，选择合适的折现率折现得到价值
    V_0=\sum_{k=1}^{n}\frac{FCFF_{k}}{(1+r_{WACC})^k}=\sum_{k=1}^{n}\frac{EBIT_{k}(1-t)+D_k-FCInv_k-WCInv_k}{(1+r_{WACC})^k}

    • 若期初投入固定/营运资本，期末回收固定/营运资本，则
      V_0=\sum_{k=1}^{n}\frac{EBIT_{k}(1-t)+D_k}{(1+r_{WACC})^k}-F\&WCInv_0+\frac{F\&WCInv_n}{(1+r_{WACC})^n}
    • 若满足UCF假设，即D_k=FCInv_k,WCInv_k=0，则
      V_0=\sum_{k=1}^{n}\frac{EBIT_{k}(1-t)}{(1+r_{WACC})^k}=\sum_{k=1}^{n}\frac{UCF_k}{(1+r_{WACC})^k}
  2. APV法：将公司价值拆分成无杠杆公司价值V_U与税盾\mathrm{PV}(It)之和
    V_0=\sum_{k=1}^{n}\frac{FCFF_{k}}{(1+r_0)^k}+\sum_{k=1}^{n}\frac{I_{k}t}{(1+r_b)^k}

    • 若期初发行永续债B_0，利息率为r_b，则
      V_0=V_U+\sum_{k=1}^{n}\frac{I_{k}t}{(1+r_b)^k}=V_U+\sum_{k=1}^{n}\frac{Br_bt}{(1+r_b)^k}=V_U+tB_0
      符合有税条件下的MM定理
    • 根据债券定价原理，由于
      \begin{align} \because\quad&0=\sum_{k=1}^{n}\frac{I_k-\Delta LTD_k}{(1+r_b)^k}=\sum_{k=1}^{n}\frac{FCFD_{k}+I_kt}{(1+r_b)^k} \\ \therefore\quad&\sum_{k=1}^{n}\frac{I_{k}t}{(1+r_b)^k}=-\sum_{k=1}^{n}\frac{FCFD_{k}}{(1+r_b)^k} \end{align}
      因此税盾价值\mathrm{PV}(It)=-\mathrm{PV}(FCFD)，APV法还可以写成
      V_0=\sum_{k=1}^{n}\frac{FCFF_{k}}{(1+r_0)^k}-\sum_{k=1}^{n}\frac{FCFD_k}{(1+r_b)^k}
    • 对于平等贷款，两种方法都能算税盾，对于不平等贷款（如优惠利率贷款），用FCFD法算税盾
  3. FTE法：计算流向股东现金流的现值得到股权价值，加上债务得到公司价值
    V_0=\sum_{k=1}^{n}\frac{FCFE_{k}}{(1+r_s)^k}+B_0=\sum_{k=1}^{n}\frac{Div_{k}-\text{新股发行}_k+\text{股票回购}_k}{(1+r_s)^k}+B_0

    • 若满足LCF假设，即Div_k=NI_k,\text{新股发行}_k=\text{股票回购}_k，则
      V_0=\sum_{k=1}^{n}\frac{NI_{k}}{(1+r_s)^k}+B_0=\sum_{k=1}^{n}\frac{LCF_{k}}{(1+r_s)^k}+B_0
  4. 税前WACC法：将公式价值拆分成无杠杆公司价值V_U^\ast与税盾\mathrm{PV}^\ast(It)之和，但拆分方法与APV法不同
    V_0=\sum_{k=1}^{n}\frac{FCFF_{k}}{(1+WACC)^k}+\sum_{k=1}^{n}\frac{I_{k}t}{(1+WACC)^k}=V_U^\ast+\sum_{k=1}^{n}\frac{I_{k}t}{(1+WACC)^k}

    • 当现金流存在增长时使用，此时债务也具有风险因此不能用r_b折现税盾，APV法计算出的税盾失效
    • 由于现金流增长时r_0=WACC，因此无杠杆公司的折现率就是WACC（增长现金流推论）
    • 由于时刻调整债务比例，税盾用r_b折现的时间趋近于0，等价于全程r_0也就是WACC折现（ME定理）

注意事项

  1. 增量现金流
    • 沉没成本：包括研发费用、调研费用，不参与资本预算
    • 税后残值：市场价值大于账面价值时，税后残值要扣除差额部分的税，反之需要加上税
    • 副效应：项目对其它项目现金流的影响，其的税后值影响现金流
    • 机会成本：机会成本产生负现金流，大小为税后值或税后残值
    • 存在安装费、运输费时，与固定资产价格一起参与折旧
    • 股利不属于增量现金流，与项目决策无关
  2. 债券/优先股资本成本
    • 市场价值 = 本息现金流折现和，因此票面利率等于无风险利率时，市值才等于面值
    • 面值不等于市值时，资本成本不再是票息率，计算YTM作为资本成本
    • 永续且面值不等于市值，r_b和r_p等于利息 / 市值
  3. 发行成本
    • 市场价值 - 发行成本 = 未来现金流折现和，从而得到资本成本
    • 永续债：r_p^\ast=\frac{r_p}{1-f_p}，优先股：r_b^\ast=\frac{r_b}{1-f_b}，普通股：r_s^\ast=\frac{D}{P(1-f_s)}+g
    • 留存收益的资本成本等于无发行成本时的权益资本成本
  4. 不同方法的要求
    • WACC法：资本结构固定
    • FTE法：资本结构固定、各期利息已知（计算FCFE需要确定I）
    • APV法：负债水平已知且不变，或各期利息已知（根据I手动计算税盾）
  5. 宣布政策时，公司价值立刻改变为政策执行后的价值，通过调整权益价值实现，而负债价值不变
    • 宣布参加项目，公司权益立刻增加NPV
    • 宣布股权融资，公司权益立刻增加融资额
    • 宣布债务融资，权益价值立刻加上税盾
  6. 债务回购与股票回购（宣布政策已调整后）
    • 债务回购股票或股票回购债务，权益与债务的价值一增一减数值相同
    • 减增股票数等于回购额除以回购价，公允回购价等于回购前后股价
  7. 只要EBIT不变，V_U就保持不变，以此作为桥梁分析资本结构改变前后的公司价值

市场操作

现金股利

  1. 基本原理
    • 资产减少
    • 所有者权益减少
      股本不变
      资本公积不变
      未分配利润减少总股利
  2. 对股价的影响
    Div(1-t_p)=(P-P^\prime)(1-t_g)\quad\Rightarrow\quad P^\prime=P-\frac{1-t_p}{1-t_g}Div

    • 无套利原理，持有股票收获的税后股利等于卖出股票再买回的税后资本利得率

股票股利

  1. 基本原理
    • 资产不变
    • 所有者权益不变
      股本增加新增股数 × 每股面值
      资本公积增加新增股数 × (市价 - 每股面值)
      未分配利润减少新增股数 × 市价
  2. 对股价的影响
    P^\prime=\frac{P}{1+\Delta\%N}

股票分割

  1. 基本原理
    • 资产不变
    • 所有者权益不变
      股本不变，但每股面值变小，流通股增加
      资本公积不变
      未分配利润不变
  2. 对股价的影响
    P^\prime=\frac{P}{1+\Delta\%N}

配股增发

  1. 基本原理
    • 配股导致所有者权益的流入，数额为配股价\times总申购数量
    • 配股导致流通股数量增加，数额为总申购数量
  2. 对资产负债表的影响
    • 资产增加，所有者权益增加
  3. 对股价的影响
    P^\prime=\frac{P+P^\ast\Delta\%N}{1+\Delta\%N}

    • P^\ast为每股配股价
    • 配股权价格：P-P^\prime

认股增发

  1. 基本原理
    • 认股导致所有者权益的流入，数额为发行价\times总申购数量
    • 认股导致流通股数量增加，数额为总申购数量
  2. 对资产负债表的影响
    • 资产增加，所有者权益增加
      P^\prime=\frac{P+P^\ast\Delta\%N}{1+\Delta\%N}
    • P^\ast为每股发行价
    • 多少份认股权能认购一股：\frac{1}{\Delta\%N}
    • 每份认股权价格：\Delta\%N(P-P^\prime)

股票回购

  1. 基本公式
    • 回购导致所有者权益的流出，数额为回购价\times总回购数量
    • 回购导致流通股数量减少，数额为总回购数量
  2. 对资产负债表的影响
    • 资产减少，负债不变，所有者权益减少
  3. 对股价的影响
    • 未给出PE时
      P^\prime=\frac{P-P^\ast\Delta\%N}{1-\Delta\%N}
      \Delta N为回购数量
      P^*为回购价格
      高于BPS回购时，股价下跌；低于BPS回购时，股价上升
    • 给出PE时
      \begin{align} &PE=\frac{P^\prime}{NI/(N-\Delta N)} \\ &P^\prime\Delta N=CF \end{align}
      CF为回购消耗的资金
      P^\prime为公允回购价，即回购后股价

发债回购

  1. 宣布发债，资金回购股票
    • 公司价值增加，增加额为税盾值
    • 权益价值增加，增加额为税盾值
    • 股价上升，总股价增加额为税盾值
  2. 回购股票
    • 债务价值增加，增加额为债务融资值
    • 权益价值减少，减小额为债务融资值
    • 股票数量减少，减少额为债务融资值除以回购价（若为公允回购，回购价应当等于宣告发债后的股价）
  3. 对股价的影响
    • 公允回购：回购股价 = 回购后的股价 = 原股价 + 债务税盾 / 股数
    • 非公允回购：回购股价 = (总权益 - 回购额) / (股数 - 回购股数)

投资融资

创业融资

  1. 下次融资时上次的现金被用完
  2. 下次融资时上次的无形资产变成其他有形资产
  3. 新融资额 / 新融资股权 = 新总权益额
  4. 等比例变动老融资额配平权益部分，增加无形资产配平资产部分

债券调换

  1. 基本原理
    • 换债项目的价值等于税后增量现金流用税后债务成本折现的现值
    • 期初债券面值与账面价值的差等于债券发行费用中资本化的部分
    • 债券摊销时，账面价值逐趋向面值
    • 回购资金超过债券账面价值时处置产生节税收入
    • 债券面值超过债券账面价值时摊销产生节税收入
  2. 期初现金流
    CF_0=B_{new}-B_{old}+(B_{old}-NBV_{old})\times t+Exp\times t

    • 发行新债的现金流入
    • 赎回旧债的现金成本
    • 旧债券超出账面价值的费用的税盾抵税
    • 发行费用的税盾抵税
  3. 交替期现金流
    CF_1=- I_{new}\times (1-t)\times \Delta T

    • 交替期多支付的新债税后利息
  4. 期间现金流
    CF_i=(I_{old}-I_{new})\times (1-t)-(Amo_{old}-Amo_{new})\times t

    • 节省的税后利息支出
    • 摊销节省导致税收增加
  5. 期末现金流
    CF_n=B_{old}-B_{new}

    • 换债导致的期末少还的本金

融资租赁

  1. 基本原理
    • 比较借款购买和融资租赁两种方法的净现值，选择净支出少的
    • 可以选择税后债务成本作为融资租赁的折现率
  2. 借款购买
    • 初始现金流：期初支付的现金
    • 期间现金流：本金和利息的流出、利息税盾的流入、折旧税盾的流入
    • 期末现金流：设备残值的收入
  3. 融资租赁
    • 期间现金流：租赁费用的流出、租赁费用的税盾的流入

并购公司

  1. 基本原理
    • 被并购公司的价值等于未来现金流的现值，收购交易的价值等于收购价格 - 被并购公司的价值
    • 若不进行融资，并购完成后权益的价值增加，增加额为被并购公司的价值，负债不变
    • 若要维持资本结构不变，必须募集被并购公司的价值 × 债务比例的债务，募集收购价格 - 被并购公司的价值 × 债务比例的资本
  2. 换股收购
    • 收购公司发行股票给被收购公司，被收购公司并入收购公司
    • 并购完成后权益的价值增加，增加额为被并购公司的价值，负债不变
    • 并购完成后股票数量增加，股价上升，发行的股票的市值就是并购的成本

其它

  1. 七二法则
    • 资金翻倍的期数约等于72除以100倍期间利率
  2. 有优先股股利时的财务杠杆
    DFL=\frac{EBIT}{EBIT-I-\frac{DIV_P}{1-t}}
  3. \beta值
    • 公司无杠杆\beta与业务无杠杆\beta均受到资本结构改变的影响
    • 公司无杠杆\beta等于各业务无杠杆\beta的按总资产加权平均
    • 股票\beta有杠杆，行业\beta无杠杆
  4. 信用条件: "2/10 n/60"
    • 表示10天内付款能有2%折扣，60天内必须付款
    • 若接收折扣，则一定选择有折扣的最后一天也就是第10天还款
    • 若放弃折扣，则一定选择最后一天也就是第60天还款，相当于第10天借入0.98，第60天付款1，机会成本为
      \frac{2\%}{1-2\%}\times\frac{360}{60-10}=14.69\%
    • 若60天内不提前付款而投资其他项目收益率大于14.69%，则选择最后一天付款
  5. 流向股东的利润：(EBIT-D\times r_d)\times(1-t)-E_p\times r_p

发表评论 取消回复
表情 图片 链接 代码

分享