第3章 差分方程、滞后运算与动态模型
3.1 一阶差分方程
3.1.1 定义
- 形式
- y_t=\alpha y_{t-1}+\varepsilon_t
- 整理得到
- y_t-y_{t-1}=(\alpha-1) y_{t-1}+\varepsilon_t
- 简写
- \Delta y_t=y_t-y_{t-1}
- \Delta\left(\Delta y_t\right)=\Delta^2y_t=\left(y_t-y_{t-1}\right)-\left(y_{t-1}-y_{t-2}\right)
3.1.2 求解
- 求解差分方程就是想要得到以随机扰动项\varepsilon_t表示的y_t的表达式
- 过程\begin{aligned} y_1& =\alpha y_0+\varepsilon_1\\ y_2& =\alpha y_1+\varepsilon_2=\alpha\left(\alpha y_0+\varepsilon_1\right)+\varepsilon_2=\alpha^2y_0+\alpha \varepsilon_1+\varepsilon_2\\ y_3& =\alpha y_2+\varepsilon_3=\alpha^3y_0+\alpha^2\varepsilon_1+\alpha \varepsilon_2+\varepsilon_3\\ y_t & =\alpha y_{t-1}+\varepsilon_t=\alpha^2y_0+\alpha^{t-1} \varepsilon_1+\alpha^{t-2} \varepsilon_2+\cdots+\varepsilon_t \\ & =\alpha^t y_0+\sum_{i=0}^{t-1} \alpha^i \varepsilon_{t-i}\end{aligned}
- 或y_t=\alpha^{t+m+1} y_{-m-1}+\sum_{i=0}^{t+m} \alpha^i \varepsilon_{t-i}
- 在|\alpha|\lt 1的条件下y_t为收敛序列,解为随机扰动项的线性函数形式
- 大于1时无法将y_t表示成随机扰动项的线性函数形式,而一阶差分方程求解结果不存在
- 等于1时为随机游走过程
- 系数\alpha影响动态走势特征
3.2 动态乘数与脉冲响应函数
3.2.1 动态乘数和影响乘数
- 定义
- 动态乘数=\frac{\partial y_{t+j}}{\partial \varepsilon_t}, \quad j=0,1,2, \cdots,描述某个随机扰动项对y的影响
- 影响乘数=\frac{\partial y_t}{\partial \varepsilon_t},特殊情况的动态乘数
- 一阶差分方程
- y_{t+j}=\alpha^{j+1} y_{t-1}+\alpha^j \varepsilon_t+\alpha^{j-1} \varepsilon_{t+1}+\cdots+\alpha \varepsilon_{t+j-1}+\varepsilon_{t+j}
- 从而\frac{\partial y_{t+j}}{\partial \varepsilon_t}=\alpha^j,与时间无关
3.2.2 脉冲响应函数
- 脉冲响应函数图
- 将动态乘数按j从小到大的顺序摆放在一起,形成的一个路径
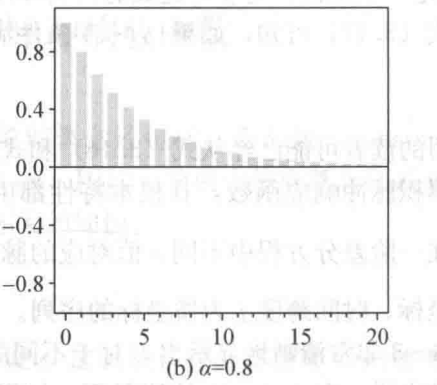
- 将动态乘数按j从小到大的顺序摆放在一起,形成的一个路径
- 累计脉冲响应函数
- 描述所有随机扰动对y的影响是脉冲响应函数的和,是所有动态乘数的和
- 衡量所有扰动项都变化一个单位后对y_{t+j}的影响
- 对于一阶差分方程
- 累计脉冲响应函数:\frac{\partial y_{t+j}}{\partial \varepsilon_t}+\frac{\partial y_{t+j}}{\partial \varepsilon_{t+1}}+\frac{\partial y_{t+j}}{\partial \varepsilon_{t+2}}+\cdots+\frac{\partial y_{t+j}}{\partial \varepsilon_{t+j}}=\alpha^j+\alpha^{j-1}+\alpha^{j-2}+\cdots+\alpha+1
- 如果|\alpha|\lt 1条件满足,累计脉冲响应函数就等于\frac{1}{1-\alpha}。此时为稳定系统,反之为不稳定系统
3.3 高阶差分方程
- 表达式
- y_t=\alpha_1y_{t-1}+\alpha_2y_{t-2}+\cdots+\alpha_p y_{t-p}+\varepsilon_t
- 矩阵形式
- \boldsymbol{Y}_t=\boldsymbol{F} \boldsymbol{Y}_{t-1}+\boldsymbol{e}_t\\
\left[\begin{array}{c}y_t \\ y_{t-1} \\ y_{t-2} \\ \vdots \\ y_{t-(p-1)}\end{array}\right]=\left[\begin{array}{ccccc}\alpha_1& \alpha_2& \alpha_3& \cdots & \alpha_p \\1&0&0& \cdots &0\\0&1&0& \cdots &0\\ \vdots & \vdots & \vdots & &0\\0&0&0&1&0\end{array}\right]\left[\begin{array}{c}y_{t-1} \\ y_{t-2} \\ y_{t-3} \\ \vdots \\ y_{t-p}\end{array}\right]+\left[\begin{array}{c}\varepsilon_t \\0\\0\\ \vdots \\0\end{array}\right]
- \boldsymbol{Y}_t=\boldsymbol{F} \boldsymbol{Y}_{t-1}+\boldsymbol{e}_t\\
- 迭代
- \boldsymbol{Y}_t=\boldsymbol{F}^{t+1} \boldsymbol{Y}_{-1}+\boldsymbol{F}^{\prime} \boldsymbol{e}_0+\boldsymbol{F}^{t-1} \boldsymbol{e}_1+\cdots+\boldsymbol{F} \boldsymbol{e}_{t-1}+\boldsymbol{e}_t
\left[\begin{array}{c}y_t \\ y_{t-1} \\ y_{t-2} \\ \vdots \\ y_{t-(p-1)}\end{array}\right]=\boldsymbol{F}^{t+1}\left[\begin{array}{c}y_{-1} \\ y_{-2} \\ y_{-3} \\ \vdots \\ y_{-p}\end{array}\right]+\boldsymbol{F}^t\left[\begin{array}{c}\varepsilon_0\\0\\0\\ \vdots \\0\end{array}\right]+\boldsymbol{F}^{t-1}\left[\begin{array}{c}\varepsilon_1\\0\\0\\ \vdots \\0\end{array}\right]+\cdots+\boldsymbol{F}\left[\begin{array}{c}\varepsilon_{t-1} \\0\\0\\ \vdots \\0\end{array}\right]+\left[\begin{array}{c}\varepsilon_t \\0\\0\\ \vdots \\0\end{array}\right] - 或:\boldsymbol{Y}_{t+j}=\boldsymbol{F}^{j+1} \boldsymbol{Y}_{t-1}+\boldsymbol{F}^j \boldsymbol{e}_t+\boldsymbol{F}^{j-1} \boldsymbol{e}_{t+1}+\cdots+\boldsymbol{F} \boldsymbol{e}_{t+j-1}+\boldsymbol{e}_{t+j}
- \boldsymbol{Y}_t=\boldsymbol{F}^{t+1} \boldsymbol{Y}_{-1}+\boldsymbol{F}^{\prime} \boldsymbol{e}_0+\boldsymbol{F}^{t-1} \boldsymbol{e}_1+\cdots+\boldsymbol{F} \boldsymbol{e}_{t-1}+\boldsymbol{e}_t
- 动态乘数
\frac{\partial y_{t+j}}{\partial \varepsilon_t}=f_{11}^{(j)}, j=0,1, \cdot- f_{11}^{(j)}表示的是矩阵\boldsymbol{F}^j的第1行第1列位置上的元素
- 动态特征本质由\boldsymbol{F}的特征根决定
3.4 滞后算子与滞后运算法
3.4.1 滞后算子定义与性质
- 规则
- L^p y_t=y_{t-p}
- 满足类指数性质
- |\alpha|\lt 1时,(1-\alpha L)^{-1}=1+\alpha L+\alpha^2L^2+\cdots
- 二阶差分方程
- y_t=\left(\alpha_1L+\alpha_2L^2\right) y_t+\varepsilon_t,等同于\left(1-\alpha_1L-\alpha_2L^2\right) y_t=\varepsilon_t,或\alpha(L) y_t=\varepsilon_t
- \alpha(L)被称为滞后算子多项式
- 考虑y_t=c+\alpha_1y_{t-1}+\alpha_2y_{t-2}+\varepsilon_t
- \left(1-\alpha_1L-\alpha_2L^2\right) y_t=c+\varepsilon_t
- y_t=\left(1-\alpha_1L-\alpha_2L^2\right)^{-1} c+\left(1-\alpha_1L-\alpha_2L^2\right)^{-1} \varepsilon_t
- 由于滞后算子不对常数项产生影响y_t=\frac{c}{1-\alpha_1-\alpha_2}+\frac{\varepsilon_t}{1-\alpha_1L-\alpha_2L^2}
- 或记成y_t=\frac{c}{\alpha(1) }+\frac{\varepsilon_t}{\alpha(L)}
- 这对任意阶差分方程都成立
3.4.2 差分方程的稳定性
- 特征方程
- 表达式为:\alpha(\lambda^{-1})=0
- 或写成:\lambda^p-\alpha_1\lambda^{p-1}-\alpha_2\lambda^{p-2}-\cdots-\alpha_p=0
- 特征方程的根均落在单位圆内时,差分方程系统就是稳定的
- 逆特征方程
- 表达式为:\alpha(z)=0
- 或写成:1-\alpha_1z^1-\alpha_2z^2-\cdots-\alpha_p z^p=0
- 特征方程的根均落在单位圆外时,差分方程系统就是稳定的
第4章 平稳AR模型
4.1 基本概念
4.1.1 随机过程与数据生成过程
- 随机过程
- 如果使用数学语言来定义随机函数,给定一个时间域T,对于T中每一个参数t,都有一个取值于确定集合W的随机变量Y_t(s),其中s属于一个特定的样本区间。所以,对于一个给定的t, Y_t(s)是一个随机变量。对于一个确定的样本s, Y_t(s)就是在s上的一组实现值,而集合\left\{Y_t(s), t \in T\right\}就是一个随机过程。
- 数据生成过程
- y_t=\beta_0x_t+\varepsilon_t, \quad \varepsilon_t \sim i.i.d.\left(0, \sigma_0^2\right), \quad t=1,2, \cdots, T
4.1.2 自协方差与自相关函数
- 自协方差\gamma_j=E\left[y_t-E\left(y_t\right)\right]\left[y_{t-j}-E\left(y_{t-j}\right)\right], j=0, \pm1, \pm2, \cdots
- 若期望值不变,则\gamma_j=E\left[y_t-\mu\right]\left[y_{t-j}-\mu\right], j=0, \pm1, \pm2, \cdots
- 此时有\operatorname{var}\left(y_t\right)=\gamma_0=E\left[y_t-\mu\right]\left[y_{t-0}-\mu\right]=E\left(y_t-\mu\right)^2
- 自相关函数(ACF)\rho_j=\frac{\operatorname{cov}\left(y_t, y_{t-j}\right)}{\sqrt{\operatorname{var}\left(y_t\right)} \sqrt{\operatorname{var}\left(y_{t-j}\right)}}, j=0, \pm1, \pm2, \cdots
- 将\rho_j相对于滞后期数j绘制出的图示称为自相关图
4.1.3 弱平稳与严平稳的定义
- 弱平稳(协方差平稳、二阶平稳)
- 期望值、方差、自协方差有限且不随时间变化
- E\left(y_t\right)=\mu为不变的常数;
- \operatorname{var}\left(y_t\right)=\gamma_0=\sigma^2为不变的常数;
- 此时显然有\gamma_j=E\left[y_t-\mu\right]\left[y_{t-j}-\mu\right], j=0, \pm1, \pm2, \cdots
- 如果组成随机过程的随机变量为弱平稳的,则这个随机过程称为弱平稳过程
- 此时有
\begin{align} &\gamma_j=\gamma_{-j}, j= \pm1, \pm2, \cdots \\ &\rho_j=\frac{\operatorname{cov}\left(y_t, y_{t-j}\right)}{\sqrt{\operatorname{var}\left(y_t\right)} \sqrt{\operatorname{var}\left(y_{t-j}\right)}}=\frac{\gamma_j}{\gamma_0}, j=0, \pm1, \pm2, \cdots \\ & \rho_0=\frac{\gamma_0}{\gamma_0}=1 \\ &\rho_j=\rho_{-j} \end{align}
- 严平稳
- 随机变量的集合和时间无关,仅和时间差有关
4.1.4 白噪音过程
- 对于所有时间t,如果满足下列条件
- \mu=0
- \gamma_0=\sigma^2
- \operatorname{cov}\left(y_t, y_{t-j}\right)=0, j \neq0
- 此时有
- \gamma_j=\left\{\begin{array}{cc}\sigma^2, & j=0\\0, & j \neq0\end{array}\right.
- \rho_j= \begin{cases}1, & j=0\\0, & j \neq0\end{cases}
- 如果白噪音满足正态分布条件,则成为高斯白噪音过程,记为\varepsilon_t \sim W N\left(0, \sigma^2\right)
4.2 一阶自回归模型:AR(1)
4.2.1 AR(1)过程的基本定义和性质
- 模型
- y_t=c+\alpha y_{t-1}+\varepsilon_t
- \varepsilon_t \sim W N\left(0, \sigma^2\right)
- 当|\alpha|\lt 1时平稳
- 平稳AR(1)等效于MA(∞)
- y_t=\frac{c}{\alpha(1) }+\frac{\varepsilon_t}{\alpha(L)}=\frac{c}{1-\alpha}+\varepsilon_t+\alpha \varepsilon_{t-1}+\alpha^2\varepsilon_{t-2}+\cdots
4.2.2 平稳AR(1)过程的均值
\mu=\frac{c}{1-\alpha}+0+0+\cdots=\frac{c}{1-\alpha}
易得:y_t=\mu+\varepsilon_t+\alpha \varepsilon_{t-1}+\alpha^2\varepsilon_{t-2}+\cdots
4.2.2 平稳AR(1)过程的方差
\begin{aligned} \gamma_0& =E\left[y_t-\mu\right]^2=E\left[\varepsilon_t+\alpha \varepsilon_{t-1}+\alpha^2\varepsilon_{t-2}+\cdots\right]^2\\ & =E\left[\varepsilon_t^2\right]+\alpha^2E\left[\varepsilon_{t-1}^2\right]+\alpha^4E\left[\varepsilon_{t-2}^2\right]+\alpha^6E\left[\varepsilon_{t-3}^2\right]+\cdots \\ & =\left(1+\alpha^2+\alpha^4+\alpha^6+\cdots\right) \sigma^2\\ & =\frac{\sigma^2}{1-\alpha^2}\end{aligned}- 均值回复:y_t服从正态分布,因此总趋向于回归到均值附近
4.2.4 平稳AR(1)过程的自协方差与自相关函数
- 自协方差
\begin{aligned} \gamma_j & =E\left[y_t-\mu\right]\left[y_{t-j}-\mu\right] \\ & =E\left[\varepsilon_t+\alpha \varepsilon_{t-1}+\alpha^2\varepsilon_{t-2}+\cdots\right]\left[\varepsilon_{t-j}+\alpha \varepsilon_{t-j-1}+\alpha^2\varepsilon_{t-j-2}+\cdots\right] \\ & =\alpha^j E\left[\varepsilon_{t-j}^2\right]+\alpha^{j+2} E\left[\varepsilon_{t-j-1}^2\right]+\alpha^{j+4} E\left[\varepsilon_{t-j-2}^2\right]+\cdots\\& =\alpha^j\left(1+\alpha^2+\alpha^4+\cdots\right) \sigma^2\\ & =\frac{\sigma^2}{1-\alpha^2} \alpha^j\end{aligned} - 自相关函数
\rho_j=\frac{\gamma_j}{\gamma_0}=\alpha^j
4.2.5 一阶自回归系数α的影响
- α越小,ACF递减越快
- α为负,ACF震荡递减
- α越大,曲线越能观察到趋势性
4.3 二阶自回归模型:AR(2)
4.3.1 AR(2)过程的基本定义和性质
- 模型
- y_t=c+\alpha_1y_{t-1}+\alpha_2y_{t-2}+\varepsilon_t
- \varepsilon_t \sim W N\left(0, \sigma^2\right)
- \lambda^2-\alpha_1\lambda-\alpha_2=0的根都落在单位圆内时平稳
- 平稳AR(2)等效于MA(∞)
- y_t=\frac{c}{\alpha(1) }+\frac{\varepsilon_t}{\alpha(L)}=\frac{c}{1-\alpha_1-\alpha_2}+\psi_0\varepsilon_t+\psi_1\varepsilon_{t-1}+\psi_2\varepsilon_{t-1}+\cdots
4.3.2 AR(2)过程的均值
\mu=\frac{c}{1-\alpha_1-\alpha_2}4.3.3 AR(2)过程的自相关函数
- 易得
y_t-\mu=\alpha_1\left(y_{t-1}-\mu\right)+\alpha_2\left(y_{t-2}-\mu\right)+\varepsilon_t - 同时乘以\left(y_{t-j}-\mu\right)并取期望
\gamma_j=\alpha_1\gamma_{j-1}+\alpha_2\gamma_{j-2} - 同时除以\gamma_0
\rho_j=\alpha_1\rho_{j-1}+\alpha_2\rho_{j-2} - 于是
\begin{align} &\rho_1=\alpha_1\rho_0+\alpha_2\rho_{-1} \\ &\rho_2=\alpha_1\rho_1+\alpha_2\rho_0 \\ &\rho_j=\rho_{-j} \\ &\rho_0=\frac{\gamma_0}{\gamma_0}=1 \end{align} - 得到
\left\{\begin{array}{l}\rho_1=\frac{\alpha_1}{1-\alpha_2} \\ \rho_2=\frac{\alpha_1^2-\alpha_2^2+\alpha_2}{1-\alpha_2}\end{array}\right. - 可以递推确定ACF
4.3.4 AR(2)过程的方差、自协方差
- 易得
y_t-\mu=\alpha_1\left(y_{t-1}-\mu\right)+\alpha_2\left(y_{t-2}-\mu\right)+\varepsilon_t - 同时乘以\left(y_{t}-\mu\right)并取期望
\gamma_0=\alpha_1\gamma_1+\alpha_2\gamma_2+\sigma^2 - 由于\gamma_1=\rho_1\gamma_0,\gamma_2=\rho_2\gamma_0,得到方差
\gamma_0=\frac{1-\alpha_2}{\left(1+\alpha_2\right)\left[\left(1-\alpha_2\right)^2-\alpha_1^2\right]} \sigma^2 - 由\gamma_i=\rho_i\gamma_0计算自协方差
4.3.5 回归系数的影响
- 考察\alpha_1+\alpha_2,结论与AR(1)类似
4.4 p阶自回归模型:AR(p)
4.4.1 AR(p)过程的基本定义和性质
- 模型
- y_t=c+\alpha_1y_{t-1}+\alpha_2y_{t-2}+\cdots+\alpha_p y_{t-p}+\varepsilon_t
- \varepsilon_t \sim W N\left(0, \sigma^2\right)
- \alpha(\lambda^{-1})=0的根都落在单位圆内时平稳
- 平稳AR(p)等效于MA(∞)
- y_t=\frac{c}{\alpha(1) }+\frac{\varepsilon_t}{\alpha(L)}=\frac{c}{1-\alpha_1-\alpha_2-\cdots-a_p}+\psi_0\varepsilon_t+\psi_1\varepsilon_{t-1}+\psi_2\varepsilon_{t-1}+\cdots
4.4.2 AR(p)过程的均值
\mu=\frac{c}{1-\alpha_1-\alpha_2-\cdots-\alpha_p}=\frac{c}{\alpha(1)}4.4.3 AR(p)过程的自相关函数
- 方法类似AR(2)
4.4.4 AR(p)过程的方差、自协方差
- 方法类似AR(2)
4.4.5 回归系数的影响
- 递减趋势主要受绝对值最大的系数影响
- 可能不完全是减函数,因为系数间的叠加可能导致下降效应被抵消
第5章 平稳 ARMA 模型
5.1 移动平均过程(MA process)
5.1.1 MA(1)模型
1. MA(1)模型的基本定义与性质
- 模型
- y_t=c+\varepsilon_t+\theta_1\varepsilon_{t-1}
- \varepsilon_i \sim W N\left(0, \sigma^2\right)
- 用滞后算子表示
- y_t=c+\left(1+\theta_1L\right) \varepsilon_t
- 因此
\begin{align} &\left(1+\theta_1L\right)^{-1}\left(y_t-c\right)=\varepsilon_t \\ &\left(1-\theta_1L+\theta_1^2L^2-\theta_1^3L^3+\cdots\right)\left(y_t-c\right)=\varepsilon_t \\ &y_t=\left(c-\theta_1c+\theta_1^2c-\theta_1^3c+\cdots\right)+\theta_1y_{t-1}-\theta_1^2y_{t-2}+\cdots+\varepsilon_t \end{align} - 这说明\left|\theta_1\right|\lt1时,MA(1)等价于AR(∞),这被称为可逆性
- MA(1)模型一定平稳,详见后文
2. MA(1)模型的期望
\mu=E\left(y_t\right)=E\left(c+\varepsilon_t+\theta_1\varepsilon_{t-1}\right)=c3. MA(1)模型的方差与自协方差
- 方差
\gamma_0=E\left[y_t-E\left(y_t\right)\right]^2=E\left(\varepsilon_t+\theta_1\varepsilon_{t-1}\right)^2=\left(1+\theta_1^2\right) \sigma^2 - 自协方差
\begin{aligned} \gamma_j&=E\left(y_t-\mu\right)\left(y_{t-j}-\mu\right) \\& =E\left(\varepsilon_t+\theta_1\varepsilon_{t-1}\right)\left(\varepsilon_{t-j}+\theta_1\varepsilon_{t-j-1}\right) \\ & =E\left(\varepsilon_t \varepsilon_{t-j}+\theta_1\varepsilon_{t-1} \varepsilon_{t-j}+\theta_1\varepsilon_t \varepsilon_{t-j-1}+\theta_1^2\varepsilon_{t-1} \varepsilon_{t-j-1}\right)\end{aligned}
因此
\gamma_j= \begin{cases}\theta_1\sigma^2, & j=1\\0, & j>1\end{cases}
4. MA(1)模型的自相关函数
\rho_j=\frac{\gamma_j}{\gamma_0}= \begin{cases}\frac{\theta_1}{1+\theta_1^2}, & j=1\\0, & j>1\end{cases}- 意味着ACF只有一阶
- 易得\left|\rho_1\right| \leqslant \frac{1}{2},在\pm 1取等
- \theta_1互为相反数时,ACF完全相同
5.1.2 MA(2)模型
1. MA(2)模型的基本定义与性质
- 模型
- y_t=c+\varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}
- \varepsilon_i \sim W N\left(0, \sigma^2\right)
- 用滞后算子表示
- y_t=c+\left(1+\theta_1L+\theta_2L^2\right) \varepsilon_t
- \lambda^2+\theta_1\lambda+\theta_2=0的根在单位圆内时,MA(2)等价于AR(∞),这被称为可逆性
- MA(2)模型一定平稳,详见后文
2. MA(2)模型的期望
\mu=E\left(y_t\right)=E\left(c+\varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}\right)=c3. MA(2)模型的方差与自协方差
- 方差
\gamma_0=E\left(y_t-\mu\right)^2=E\left(\varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}\right)^2=\left(1+\theta_1^2+\theta_2^2\right) \sigma^2 - 自协方差
\begin{aligned} \gamma_j&=E\left(y_t-\mu\right)\left(y_{t-j}-\mu\right) \\ & =E\left(\varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}\right)\left(\varepsilon_{t-j}+\theta_1\varepsilon_{t-j-1}+\theta_2\varepsilon_{t-j-2}\right) \\ & =E\left(\varepsilon_t \varepsilon_{t-j}+\theta_1\varepsilon_{t-1} \varepsilon_{t-j}+\theta_1\varepsilon_t \varepsilon_{t-j-1}+\theta_1^2\varepsilon_{t-1} \varepsilon_{t-j-1}+\cdots\right)\end{aligned}
因此
\gamma_j= \begin{cases}\theta_1\left(1+\theta_2\right) \sigma^2, & j=1\\ \theta_2\sigma^2, & j=2\\0, & j>2\end{cases}
4. MA(2)模型的自相关函数
\rho_j=\frac{\gamma_j}{\gamma_0}= \begin{cases}\frac{\theta_1\left(1+\theta_2\right)}{1+\theta_1^2+\theta_2^2}, & j=1\\ \frac{\theta_2}{1+\theta_1^2+\theta_2^2}, & j=2\\0, & j>2\end{cases}- 意味着ACF只有二阶
- 易得\left|\rho_1\right| \leqslant \frac{\sqrt{2}}{2},在\theta_1=\pm\sqrt{2}, \quad \theta_2=1取等
5.1.3 MA(q)模型
1. MA(q)模型的基本定义与性质
- 模型
- y_t=c+\varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}+\cdots+\theta_q \varepsilon_{t-q}
- \varepsilon_i \sim W N\left(0, \sigma^2\right)
- 用滞后算子表示
- y_t=c+\left(1+\theta_1L+\theta_2L^2+\cdots+\theta_qL^q\right) \varepsilon_t
- \theta(\lambda^{-1})=0的根在单位圆内时,MA(q)等价于AR(∞),这被称为可逆性
- MA(q)模型一定平稳,详见后文
2. MA(q)模型的期望
\mu=E\left(c+\varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}+\cdots+\theta_q \varepsilon_{t-q}\right)=c3. MA(q)模型的方差与自协方差
- 方差
\gamma_0=\left(1+\theta_1^2+\theta_2^2+\cdots+\theta_q^2\right) \sigma^2 - 自协方差
\begin{aligned} \gamma_j & =E\left(y_t-\mu\right)\left(y_{t-j}-\mu\right) \\ & =E\left(\varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}+\cdots+\theta_q \varepsilon_{t-q}\right)\left(\varepsilon_{t-j}+\theta_1\varepsilon_{t-j-1}+\theta_2\varepsilon_{t-j-2}+\cdots+\theta_q \varepsilon_{t-j-q}\right) \\ & =E\left(\theta_j \varepsilon_{t-j}^2+\theta_{j+1} \theta_1\varepsilon_{t-j-1}^2+\theta_{j+2} \theta_2\varepsilon_{t-j-2}^2+\cdots+\theta_q \theta_{q-j} \varepsilon_{t-q}^2\right)\end{aligned}
因此
\gamma_j= \begin{cases}\left(\theta_j+\theta_{j+1} \theta_1+\theta_{j+2} \theta_2+\cdots+\theta_q \theta_{q-j}\right) \sigma^2, & j=1,2, \cdots, q \\0, & j>q\end{cases}
4. MA(q)模型的自相关函数
\rho_j= \begin{cases}\frac{\theta_j+\theta_{j+1} \theta_1+\theta_{j+2} \theta_2+\cdots+\theta_q \theta_{q-j}}{1+\theta_1^2+\theta_2^2+\cdots+\theta_q^2}, & j=1,2, \cdots, q \\0, & j>q\end{cases}- 意味着ACF只有q阶
5.2 自回归移动平均过程(ARMA process)
5.2.1 ARMA(p,q)过程的基本定义
- 模型
- y_t=c+\alpha_1y_{t-1}+\alpha_2y_{t-2}+\cdots+\alpha_p y_{t-p}+\varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}+\cdots+\theta_q \varepsilon_{t-q}
- \varepsilon_i \sim W N\left(0, \sigma^2\right)
- 用滞后算子表示
- \left(1-\alpha_1L-\alpha_2L^2-\cdots-\alpha_p L^p\right) y_t=c+\left(1+\theta_1L+\theta_2L^2+\cdots+\theta_q L^q\right) \varepsilon_t
- 记为\alpha(L) y_t=c+\theta(L) \varepsilon_t
5.2.2 ARMA(p,q)过程的平稳性与可逆性
- 平稳性
- \alpha(\lambda^{-1})=0的根都在单位圆内
- 如果有根落在单位圆上,则为自回归单整移动平均过程ARIMA(p,d,q),d为单整阶数
- 可逆性
- \theta(\lambda^{-1})=0的根都在单位圆内
5.2.3 ARMA(p,q)过程的均值、方差与自协方差
- 均值
\mu=\frac{c}{1-\alpha_1L-\alpha_2L^2-\cdots-\alpha_p L^p}=\frac{c}{\alpha(1)} - 方差
- 易得
y_t-\mu= \alpha_1\left(y_{t-1}-\mu\right)+\alpha_2\left(y_{t-2}-\mu\right)+\cdots+\alpha_p\left(y_{t-p}-\mu\right)+\left(\varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}+\cdots+\theta_q \varepsilon_{t-q}\right) - 同乘以y_{t-j}-\mu并取期望
\begin{aligned} \gamma_j= & E\left(y_t-\mu\right)\left(y_{t-j}-\mu\right) \\ = & E\left[\alpha_1\left(y_{t-1}-\mu\right)\left(y_{t-j}-\mu\right)+\alpha_2\left(y_{t-2}-\mu\right)\left(y_{t-j}-\mu\right)+\cdots\right. \\ & \left.+\alpha_p\left(y_{t-p}-\mu\right)\left(y_{t-j}-\mu\right)+\left(\varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}+\cdots+\theta_q \varepsilon_{t-q}\right)\left(y_{t-j}-\mu\right)\right] \\ = & \alpha_1\gamma_{j-1}+\alpha_2\gamma_{j-2}+\cdots+\alpha_p \gamma_{j-p} \\ & +E\left[\left(\varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}+\cdots+\theta_q \varepsilon_{t-q}\right)\left(y_{t-j}-\mu\right)\right] \\ = & \alpha_1\gamma_{j-1}+\alpha_2\gamma_{j-2}+\cdots+\alpha_p \gamma_{j-p} \\ & +E\left(\varepsilon_t y_{t-j}\right)+\theta_1E\left(\varepsilon_{t-1} y_{t-j}\right)+\theta_2E\left(\varepsilon_{t-2} y_{t-j}\right)+\cdots+\theta_q E\left(\varepsilon_{t-q} y_{t-j}\right)\end{aligned}
- 易得
5.2.4 ARMA(p,q)过程的自相关函数
- j\gt q时
- 根据自协方差表达式
\gamma_j=\alpha_1\gamma_{j-1}+\alpha_2\gamma_{j-2}+\cdots+\alpha_p \gamma_{j-p}, \quad j=q+1, q+2, \cdots - 自相关函数为
\rho_j=\alpha_1\rho_{j-1}+\alpha_2\rho_{j-2}+\cdots+\alpha_p \rho_{j-p}, \quad j=q+1, q+2, \cdots - 此时ACF表现与AR(p)相同
- 根据自协方差表达式
- j\le q时
- ACF受AR与MA共同作用
- 如ARMA(p,q)
\rho_j= \begin{cases}\frac{\left(1+\alpha_1\theta_1\right)\left(\alpha_1+\theta_1\right)}{1+\theta_1^2+2\alpha_1\theta_1}, & j=1\\\alpha_1\rho_{j-1}, & j>1\end{cases}
5.2.5 AR与 MA 模型的互相转化
- 由模型
\alpha(L) y_t=c+\theta(L) \varepsilon_t - 得到MA模型
y_t=\alpha(L)^{-1}\left[c+\theta(L) \varepsilon_t\right]=\frac{c}{\alpha(1)}+\left[\alpha(L)^{-1} \theta(L)\right] \varepsilon_t=\frac{c}{\alpha(1)}+\varphi(L) \varepsilon_t- 只要\alpha(L)\ne 1,就是MA(∞)模型
- 得到AR模型
\begin{align} &\theta(L)^{-1} \alpha(L) y_t=\theta(L)^{-1} c+\varepsilon_t \\ &\vartheta(L) y_t=\frac{c}{\theta(1)}+\varepsilon_t \end{align}- 只要\theta(L)\ne 1,就是AR(∞)模型
5.3 部分自相关函数(partial autocorrelation)
- ACF描述了不同项之间的关系,但这种关系受其他项影响
- PACF值描述两项之间的关系,排除了其它项的影响
- 例如,对于AR(1),因为模型只考虑一阶前项,因此PACF图只有一期,但ACF确有无数期
- 表达式
- 第k项记为\phi_{k k}
- 显然,根据定义,可以用OLS计算
y_t=\mu+\phi_{k1} y_{t-1}+\phi_{k2} y_{t-2}+\cdots+\phi_{k k} y_{t-k}+e_t - 或者,根据ACF计算
某一期的ACF可以看做其它期的ACF的线性组合,权重为\phi_{k i}
\gamma_j=\phi_{k1} \gamma_{j-1}+\phi_{k2} \gamma_{j-2}+\cdots+\phi_{k k} \gamma_{j-k}
于是
\left[\begin{array}{c}\phi_{k1} \\ \phi_{k2} \\ \vdots \\ \phi_{k k}\end{array}\right]=\left[\begin{array}{cccc}\gamma_0& \gamma_1& \cdots & \gamma_{k-1} \\ \gamma_1& \gamma_0& \cdots & \gamma_{k-2} \\ \vdots & \vdots & & \vdots \\ \gamma_{k-1} & \gamma_{k-2} & \cdots & \gamma_0\end{array}\right]^{-1}\left[\begin{array}{c}\gamma_1\\ \gamma_2\\ \vdots \\ \gamma_k\end{array}\right]
或者
\left[\begin{array}{c}\phi_{k1} \\ \phi_{k2} \\ \vdots \\ \phi_{k k}\end{array}\right]=\left[\begin{array}{cccc}1& \rho_1& \cdots & \rho_{k-1} \\ \rho_1&1& \cdots & \rho_{k-2} \\ \vdots & \vdots & & \vdots \\ \rho_{k-1} & \rho_{k-2} & \cdots &1\end{array}\right]^{-1}\left[\begin{array}{c}\rho_1\\ \rho_2\\ \vdots \\ \rho_k\end{array}\right]
可得
\phi_{k k}=\frac{\rho_k-\sum_{j=1}^{k-1} \phi_{k-1, j} \rho_{k-j}}{1-\sum_{j=1}^{k-1} \phi_{k-1, j} \rho_j}, k>1 - \phi_{11}=\rho_1
- \phi_{22}=\frac{\rho_2-\rho_1^2}{1-\rho_1^2}
- AR与MR的PACF

5.4 样本自相关与部分自相关函数
5.4.1样本自相关函数(SACF)
- 计算估计量
\left\{\begin{array}{l}\bar{y}=\frac{1}{T} \sum_{t=1}^T y_t \\ \hat{\sigma}^2=\frac{1}{T} \sum_{t=1}^T\left(y_t-\bar{y}\right)^2\\ \hat{\gamma}_j=\frac{1}{T} \sum_{t=j+1}^T\left(y_t-\bar{y}\right)\left(y_{t-j}-\bar{y}\right)\end{array}\right. - 得到SACF
\hat{\rho}_j=\frac{\hat{\gamma}_j}{\hat{\gamma}_0}=\frac{\sum_{t=j+1}^T\left(y_t-\bar{y}\right)\left(y_{t-j}-\bar{y}\right)}{\sum_{t=j+1}^T\left(y_t-\bar{y}\right)^2} - Ljung-Box Q检验
- 原假设:待检验的变量从1至j期没有自相关性,即\hat{\rho}_i=0
- 统计量:
Q=T(T+2) \sum_{j=1}^k \frac{\hat{\rho}_j^2}{T-j}\sim\chi_{df}^2 - Q\gt\chi_{1-\alpha,df}^2时拒绝
- 其中, \rho_j是第j期的自相关函数, T代表有效观测值的个数(即样本大小)
- 对于ARMA(p,q),由于有常数项,自由度为k-p-q-1
5.4.2 样本部分自相关函数(SPACF)
- 利用SACF估计
\hat{\phi}_{k k}=\frac{\hat{\rho}_k-\sum_{j=1}^{k-1} \hat{\phi}_{k-1, j} \hat{\rho}_{k-j}}{1-\sum_{j=1}^{k-1} \hat{\phi}_{k-1, j} \hat{\rho}_j}- 是一致近似值
- 采用OLS方法可以得到更精确的估计值
5.5 自相关性检验
判断模型的随机误差项是否存在自相关现象
5.5.1 Breusch-Godfrey LM序列相关性检验
- 设模型为y_t=c+\alpha_1y_{t-1}+\cdots+\alpha_p y_{t-p}+u_t,估计原模型得到残差序列\hat{u}_t
- 对下面方程进行回归
y_t=c+\alpha_1y_{t-1}+\cdots+\alpha_p y_{t-p}+\phi_1\hat{u}_{t-1}+\phi_2\hat{u}_{t-2}+\cdots+\phi_m \hat{u}_{t-m}+\varepsilon_t- 若\hat{u}_i不存在,则视为0
- 原假设为H_0: \phi_1=\phi_2=\cdots=\phi_m=0,即不存在序列相关性
- 计算回归的R^2
- 检验统计量:(T-m)R^2\sim \chi_m^2
- 检验统计量\gt\chi_{1-\alpha,m}^2时拒绝
5.5.2 Durbin-Watson 序列相关性检验
- 设模型为y_t=c+\alpha_1x_{1,t}+\cdots+\alpha_p x_{p,t}+u_t,估计原模型得到残差序列\hat{u}_t
- 原假设为不存在一阶序列相关性
- 检验统计量
\begin{align} d&=\frac{\sum_{t=2}^T\left(\hat{u}_t-\hat{u}_{t-1}\right)^2}{\sum_{t=1}^T\left(\hat{u}_t\right)^2} \\ &\approx \frac{2\left(\sum_{t=2}^T\left(\hat{u}_t\right)^2-\sum_{t=2}^T\left(\hat{u}_t \hat{u}_{t-1}\right)\right)}{\sum_{t=1}^T\left(\hat{u}_t\right)^2} \\ &=2(1-\frac{\sum_{t=2}^T\left(\hat{u}_t \hat{u}_{t-1}\right)}{\sum_{t=1}^T\left(\hat{u}_t\right)^2}) \\ &=2(1-\hat{\rho}) \end{align}

- 检验统计量
- 缺点
- 只能检验残差是否一阶自相关
- 解释变量不能包含滞后项
- 存在两个不能判别的区域
5.6 ARMA 模型的实证分析及应用
5.6.1 ARMA 模型的滞后期设立
- Box-Jenkins 模型选择原则
- 模型具有较好的拟合优度,且滞后期数不会过大
- 向下检验法
- 选择一个最大滞后期,设立模型
- 检验最后一个滞后项的系数是否显著,若不显著,则去掉该项,重复此步骤
- 知道最后一个滞后项的系数显著,此时即为最优AR模型
- 对最大滞后期的选择很重要,对于季度数据,推荐8或4
- 信息准则法
- AIC和SIC
\begin{aligned} & \operatorname{AIC}(p)=\ln \left(\frac{\sum_{t=1}^T \varepsilon_t^2}{T_s}\right)+\frac{2p}{T_s} \\ & \operatorname{SIC}(p)=\ln \left(\frac{\sum_{t=1}^T \varepsilon_t^2}{T_s}\right)+\frac{p \ln \left(T_s\right)}{T_s}\end{aligned} - 选择AIC或SIC最小时的p值
- AIC与SIC的判断结果可能不一致,通常AIC的更大,可以采用向下检验法,并判断残差是否自相关
- AIC和SIC
5.6.2 ARMA 模型的回归估计
- 对于AR(p)模型,有效观测值个数会减少p个
- 对于MA模型,OLS是无效的,需要采用非线性OLS即NLS
第6章 预测理论与应用
6.1 基本概念与预测初步
6.1.1 基本概念
预测信息集
- 单变量信息集:只考虑被预测变量的历史数据
\Omega_T=\left\{y_T, y_{T-1}, y_{T-2}, \cdots, y_1\right\} - 多变量信息集:还考虑对预测变量可能有影响的其他变量的数据
\Omega_T=\left\{y_T, y_{T-1}, y_{T-2}, \cdots, y_1, x_T, x_{T-1}, x_{T-2}, \cdots, x_1\right\}
预测期
- 当前时间为T,预测T+n的数据,则预测期为n
最优预测
- 在给定信息集下,预测结果能够最小化预测损失
- 给定信息集下的条件期望E\left(y_{T+h} \mid \Omega_T\right)就是最优预测
6.1.2 预测初步:基于时间趋势模型的预测
- 线性时间趋势模型
y_t=c+\beta t+\varepsilon_t - 非线性时间趋势模型
y_t=c+\beta_1t+\beta_2t^2+\varepsilon_t - 基于时间趋势模型的预测分析
y_{T+h}=c+\beta(T+h)+\varepsilon_{T+h}
6.2 基于MA(2)模型的预测
- 预测模型
y_{T+1}=\varepsilon_{T+1}+\theta_1\varepsilon_T+\theta_2\varepsilon_{T-1} - 点预测
- T之后的扰动项视为0
\left\{\begin{array}{l} y_{T+1, T}=P\left(y_{T+1} \mid \Omega_T\right)=0+\theta_1\varepsilon_T+\theta_2\varepsilon_{T-1} \\ y_{T+2, T}=P\left(y_{T+2} \mid \Omega_T\right)=0+0+\theta_2\varepsilon_T=\theta_2\varepsilon_T \\ \cdots \\ y_{T+h, T}=P\left(y_{T+h} \mid \Omega_T\right)=0 \end{array}\right.
- T之后的扰动项视为0
- 预测误差
- e_{T+h, T}=y_{T+h}-y_{T+h, T}
\left\{\begin{array}{l}e_{T+1, T}=\varepsilon_{T+1}(h=1) \\ e_{T+2, T}=\varepsilon_{T+2}+\theta_1\varepsilon_{T+1}(h=2) \\ \cdots \\ e_{T+h, T}=\varepsilon_{T+h}+\theta_1\varepsilon_{T+h-1}+\theta_2\varepsilon_{T+h-2}(h>2)\end{array}\right. - 方差
\left\{\begin{array}{l}\sigma_1^2=\sigma^2\\ \sigma_2^2=\sigma^2\left(1+\theta_1^2\right) \\ \cdots \\ \sigma_h^2=\sigma^2\left(1+\theta_1^2+\theta_2^2\right)(h>2)\end{array}\right.
- e_{T+h, T}=y_{T+h}-y_{T+h, T}
6.3 基于AR(1)模型的预测
- 预测模型
y_{T+1}=\alpha y_T+\varepsilon_{T+1} - 点预测
- T之后的扰动项视为0
\left\{\begin{array}{l} y_{T+1, T}=\alpha y_T+0=\alpha y_T \\ y_{T+2, T}=\alpha y_{T+1}+0=\alpha y_{T+1,T} \\ \cdots \\ y_{T+h, T}=\alpha y_{T+h}+0=\alpha y_{T+h-1,T} \end{array}\right. - 使用预测值预测下一期称为动态预测;使用真实值预测下一期称为静态预测(前提是有观察数据)
- T之后的扰动项视为0
- 预测误差
- e_{T+h, T}=y_{T+h}-y_{T+h, T}=\varepsilon_t+\alpha \varepsilon_{t-1}+\alpha^2\varepsilon_{t-2}+\cdots
- 方差:\sigma^2\sum_{i=0}^{h-1} \alpha^{2i}
6.4 预测准确性的度量指标
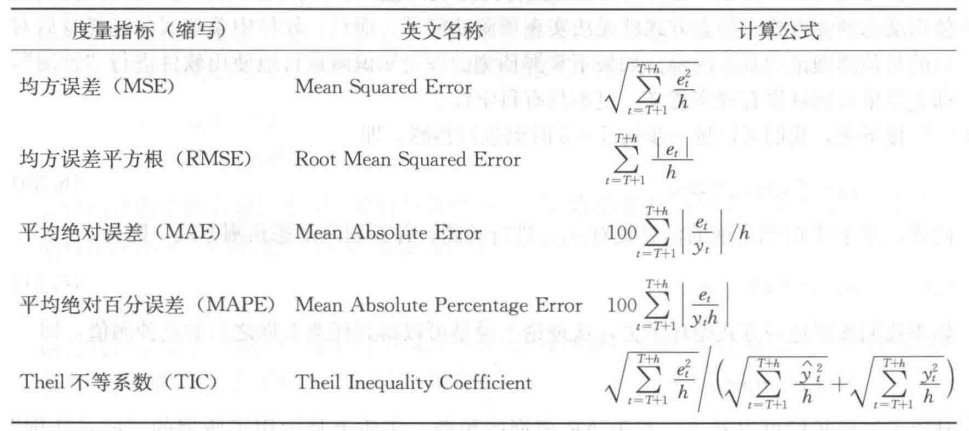
第7章 非平稳时间序列模型
7.1 确定性趋势模型
- 模型中明确含有时间变量,如
y_t=c+\beta t+u_t, t=1,2, \cdots- 其中u_t只需要是平稳变量,可以存在序列相关性
- 此时y_t是均值非平稳过程,而y_t-E\left(y_t\right)=u_t是平稳过程
- 一般的
y_t-E\left(y_t\right)=\varphi(L) u_t
7.2 随机趋势模型
7.2.1 随机趋势模型的基本定义
- 扰动项产生永久影响
- 如y_t=y_{t-1}+\varepsilon_t,因为y_t=y_0+\sum_{i=1}^t \varepsilon_i
7.2.2 随机游走模型
- 模型
\begin{align} &y_t=y_{t-1}+\varepsilon_t \\ &y_t=\left(y_0+\sum_{i=1}^t \varepsilon_i\right) \end{align} - 均值
\mu_t=E\left(y_0+\sum_{i=1}^t \varepsilon_i\right)=y_0 - 方差
\gamma_{0,t}=\operatorname{var}\left(y_0+\sum_{i=1}^t \varepsilon_i\right)=t \sigma^2- 可见随机游走过程是非平稳时间序列
- 自协方差函数
\begin{aligned} \gamma_{j,t} & =E\left[y_t-y_0\right]\left[y_{t-j}-y_0\right] \\ & =E\left[\left(\varepsilon_t+\varepsilon_{t-1}+\cdots+\varepsilon_1\right)\left(\varepsilon_{t-j}+\varepsilon_{t-j-1}+\cdots+\varepsilon_1\right)\right] \\ & =E\left(\varepsilon_{t-j}^2+\varepsilon_{t-j-1}^2+\cdots+\varepsilon_1^2\right) \\ & =(t-j) \sigma^2\end{aligned} - 自相关函数
\begin{aligned} \rho_{j,t} & =\frac{\gamma_{j,t}}{\sqrt{\operatorname{var}\left(y_t\right) \operatorname{var}\left(y_{t-j}\right)}} \\ & =\frac{(t-j) \sigma^2}{\sqrt{t \sigma^2(t-j) \sigma^2}} \\ & =\frac{t-j}{\sqrt{t(t-j)}} \\ & =\left(\frac{t-j}{t}\right)^{\frac{1}{2}}\end{aligned}- ACF从接近1开始递减,类似AR模型
7.2.3 带有截距项的随机游走模型
- 模型
\begin{align} &y_t=c+y_{t-1}+\varepsilon_t \\ &y_t=c t+\left(y_0+\sum_{i=1}^t \varepsilon_i\right) \end{align} - 均值
\mu_t=y_0+c t - 方差
\begin{aligned} \gamma_{0,t}& =E\left[y_t-E\left(y_t\right)\right]^2\\ & =E\left[y_0+c t+\varepsilon_1+\varepsilon_2+\cdots+\varepsilon_t-\left(y_0+c t\right)\right]^2\\ & =E\left(\varepsilon_1+\varepsilon_2+\cdots+\varepsilon_t\right)^2\\ & =E\left(\varepsilon_1\right)^2+E\left(\varepsilon_2\right)^2+\cdots+E\left(\varepsilon_t\right)^2\\ & =t \sigma^2\end{aligned}- 与随机游走过程相同
- 自协方差
\begin{aligned} \gamma_{j,t} & =E\left[y_t-E\left(y_t\right)\right]\left[y_{t-j}-E\left(y_{t-j}\right)\right] \\ & =E\left[\left(\varepsilon_t+\varepsilon_{t-1}+\cdots+\varepsilon_1\right)\left(\varepsilon_{t-j}+\varepsilon_{t-j-1}+\cdots+\varepsilon_1\right)\right] \\ & =E\left(\varepsilon_{t-j}^2+\varepsilon_{t-j-1}^2+\cdots+\varepsilon_1^2\right) \\ & =(t-j) \sigma^2\end{aligned}- 与随机游走过程相同
- 自相关函数
\begin{aligned} \rho_{j,t} & =\frac{\gamma_j}{\sqrt{\operatorname{var}\left(y_t\right) \operatorname{var}\left(y_{t-j}\right)}} \\ & =\frac{(t-j) \sigma^2}{\sqrt{t \sigma^2(t-j) \sigma^2}} \\ & =\left(\frac{t-j}{t}\right)^{\frac{1}{2}}\end{aligned}- 与随机游走过程相同
7.3 去除趋势的方法
- 平稳时间序列的特性
- 随机冲击的影响是暂时的,随时间推移而减弱
- 均值回复
- 非平稳时间序列的特性
- 没有均值回复
- 随机扰动的影响是长久的
- 许多经典回归的假设不能被满足
- 容易出现伪回归
- 有的条件下需要进行协整分析
7.3.1 差分法
- 单整过程
- 随机游走过程又叫单位根过程,或者一阶单整过程,记作I(1)
- 类似的,对于有两个单位根的AR模型,记作I(2)
- 对于n阶单整过程,差分n次后可以变成平稳过程
- 例如对于随机游走,\Delta y_t=\varepsilon_t
- 类似的,对于有截距项的随机游走,一次差分也能变成平稳过程
- \Delta y_t=c+\varepsilon_t
- \mu=c
- \gamma_0=E\left(\Delta y_t-c\right)^2=\sigma^2
- \gamma_j=\operatorname{cov}\left(\Delta y_t, \Delta y_{t-j}\right)=E\left[\left(\Delta y_t-c\right)\left(\Delta y_{t-j}-c\right)\right]=0
- ARIMA(p,d,q)模型
- 对于\alpha(L) y_t=\theta(L) \varepsilon_t,进行d阶差分变成ARMA(p-d,q)模型
\begin{align} &\alpha(L) y_t=\theta(L) \varepsilon_t \\ &\frac{\alpha(L)}{(1-L)^d} \Delta^d y_t=\theta(L) \varepsilon_t \end{align}
- 对于\alpha(L) y_t=\theta(L) \varepsilon_t,进行d阶差分变成ARMA(p-d,q)模型
7.3.2 去除趋势法
- 差分法有时无效,如对y_t=c+\beta t+\varepsilon_t,差分后为不可逆MA过程
- 对于确定性趋势模型,应当去除时间趋势
- 对于
y_t=c+\beta_1t+\beta_2t^2+\cdots+\beta_m t^m+\varepsilon_t - 首先估计
\hat{y}_t=\hat{c}+\hat{\beta}_1t+\hat{\beta}_2t^2+\cdots+\hat{\beta}_m t^m - 作差得到平稳过程
y_t-\hat{y}_t=\hat{\varepsilon}_t - 可以通过向下检验法得到最佳m值
- 对于
第9章 向量自回归(VAR)模型
9.1 VAR模型介绍
9.1.1 VAR模型的基本概念
- VAR模型不区分内生变量与外生变量,所有变量都会受到其它变量的所有期的影响
- 对于n个时间序列变量构成的向量\boldsymbol{Y}_t=[y_{1t},y_{2t},\cdots,y_{nt}]^{\prime},VAR(p)模型为
\boldsymbol{Y}_t=\boldsymbol{C}+\boldsymbol{\Phi}_1\boldsymbol{Y}_{t-1}+\boldsymbol{\Phi}_2\boldsymbol{Y}_{t-2}+\cdots+\boldsymbol{\Phi}_p \boldsymbol{Y}_{t-p}+\boldsymbol{\varepsilon}_t - \boldsymbol{\varepsilon}_t代表n \times1维的向量白噪音
\begin{aligned} & E\left(\boldsymbol{\varepsilon}_t\right)=\mathbf{0} \\ & E\left(\boldsymbol{\varepsilon}_t^{\prime} \boldsymbol{\varepsilon}_t^{\prime}\right)=\boldsymbol{\Omega} \\ & E\left(\boldsymbol{\varepsilon}_t^{\prime} \boldsymbol{\varepsilon}_s^{\prime}\right)=\mathbf{0} \text {,对于} s \neq t\end{aligned}
- 对于n个时间序列变量构成的向量\boldsymbol{Y}_t=[y_{1t},y_{2t},\cdots,y_{nt}]^{\prime},VAR(p)模型为
- 用滞后算子表示
\begin{align} &\boldsymbol{\Phi}(L) \boldsymbol{Y}_t=\boldsymbol{C}+\boldsymbol{\varepsilon}_t \\ &\boldsymbol{\Phi}(L)=\boldsymbol{I}_n-\boldsymbol{\Phi}_1L-\boldsymbol{\Phi}_2L^2-\cdots-\boldsymbol{\Phi}_p L^p \end{align}
9.1.2 VAR 模型的平稳性条件
- 条件:与时间无关
- E\left(\boldsymbol{Y}_t\right)=\boldsymbol{\mu}
- E\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)^{\prime}=\boldsymbol{\Gamma}_0
- E\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)\left(\boldsymbol{Y}_{t-j}-\boldsymbol{\mu}\right)^{\prime}=\boldsymbol{\Gamma}_j
- \boldsymbol{\Gamma}为自协方差矩阵
- 判断方法
- |\boldsymbol{\Phi}(\lambda^{-1})|=0的根都落在单位圆外
- |\boldsymbol{\Phi}(z)|=0的根都落在单位圆外
9.1.3 VAR(p)模型与VAR(1)的转化
- 由于均值恒定,取期望得
\boldsymbol{\mu}=\boldsymbol{C}+\boldsymbol{\Phi}_1\boldsymbol{\mu}+\boldsymbol{\Phi}_2\boldsymbol{\mu}+\cdots+\boldsymbol{\Phi}_p \boldsymbol{\mu} - 解得
\boldsymbol{\mu}=\left(\boldsymbol{I}_{\boldsymbol{n}}-\boldsymbol{\Phi}_1-\boldsymbol{\Phi}_2-\cdots-\boldsymbol{\Phi}_p\right)^{-1} \boldsymbol{C} - 于是有
\boldsymbol{Y}_t-\boldsymbol{\mu}=\boldsymbol{\Phi}_1\left(\boldsymbol{Y}_{t-1}-\boldsymbol{\mu}\right)+\boldsymbol{\Phi}_2\left(\boldsymbol{Y}_{t-2}-\boldsymbol{\mu}\right)+\cdots+\boldsymbol{\Phi}_p\left(\boldsymbol{Y}_{t-p}-\boldsymbol{\mu}\right)+\boldsymbol{\varepsilon}_t - 得到
\begin{align} &\overline{\boldsymbol{Y}}_t=\boldsymbol{F} \overline{\boldsymbol{Y}}_{t-1}+\boldsymbol{V}_t \\ &\left[\begin{array}{l}\boldsymbol{Y}_t-\mu \\ \boldsymbol{Y}_{t-1}-\mu \\ \vdots \\ \boldsymbol{Y}_{t-(p-1)}-\mu\end{array}\right]=\left[\begin{array}{cccccc}\boldsymbol{\Phi}_1& \boldsymbol{\Phi}_2& \boldsymbol{\Phi}_3& \cdots & \boldsymbol{\Phi}_{p-1} & \boldsymbol{\Phi}_p \\ \boldsymbol{I}_n & \mathbf{0} & \mathbf{0} & \cdots & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{I}_n & \mathbf{0} & \cdots & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \boldsymbol{I}_n & \cdots & \mathbf{0} & \mathbf{0} \\ \vdots & \vdots & \vdots & & \vdots & \vdots \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \cdots & \boldsymbol{I}_n & \mathbf{0}\end{array}\right]\left[\begin{array}{l}\boldsymbol{Y}_{t-1}-\mu \\ \boldsymbol{Y}_{t-2}-\mu \\ \vdots \\ \boldsymbol{Y}_{t-p}-\mu\end{array}\right]+\left[\begin{array}{c}\boldsymbol{\varepsilon}_t \\ \mathbf{0} \\ \vdots \\ \mathbf{0}\end{array}\right] \end{align}- 其中
\begin{align} \left\{\begin{array}{l}E\left(\boldsymbol{V}_t \boldsymbol{V}_t^{\prime}\right)=\boldsymbol{E} \\ E\left(\boldsymbol{V}_t \boldsymbol{V}_s^{\prime}\right)=\mathbf{0}, \text {对于} t \neq s\end{array}\right. \\ \boldsymbol{E}_{n p \times n p}=\left[\begin{array}{cccc}\boldsymbol{\Omega} & \mathbf{0} & \cdots & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \cdots & \mathbf{0} \\ \vdots & \vdots & & \vdots \\ \mathbf{0} & \mathbf{0} & \cdots & \mathbf{0}\end{array}\right] \end{align}
- 其中
9.1.4 向量自协方差和向量自相关函数
- 表达式
\begin{aligned} \boldsymbol{\Gamma}_j= & E\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)\left(\boldsymbol{Y}_{t-j}-\boldsymbol{\mu}\right)^{\prime} \\ = & \boldsymbol{\Phi}_1E\left(\boldsymbol{Y}_{t-1}-\boldsymbol{\mu}\right)\left(\boldsymbol{Y}_{t-j}-\boldsymbol{\mu}\right)^{\prime}+\boldsymbol{\Phi}_2E\left(\boldsymbol{Y}_{t-2}-\boldsymbol{\mu}\right)\left(\boldsymbol{Y}_{t-j}-\boldsymbol{\mu}\right)^{\prime}+\cdots \\ & +\boldsymbol{\Phi}_p E\left(\boldsymbol{Y}_{t-p}-\boldsymbol{\mu}\right)\left(\boldsymbol{Y}_{t-j}-\boldsymbol{\mu}\right)^{\prime}+E\left[\boldsymbol{\varepsilon}_t\left(\boldsymbol{Y}_{t-j}-\boldsymbol{\mu}\right)^{\prime}\right] \\ = & \boldsymbol{\Phi}_1\boldsymbol{\Gamma}_{j-1}+\boldsymbol{\Phi}_2\boldsymbol{\Gamma}_{j-2}+\cdots+\boldsymbol{\Phi}_p \boldsymbol{\Gamma}_{j-p}, \text {对于} j>1\end{aligned}- 利用\left[\boldsymbol{\varepsilon}_t\left(\boldsymbol{Y}_{t-j}-\boldsymbol{\mu}\right)^{\prime}\right]=0
- 性质
\begin{aligned} & \boldsymbol{\Gamma}_j^{\prime}=E\left[\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)\left(\boldsymbol{Y}_{t-j}-\boldsymbol{\mu}\right)^{\prime}\right]^{\prime} \\ & \quad=E\left[\left(\boldsymbol{Y}_{t-j}-\boldsymbol{\mu}\right)\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)^{\prime}\right] \\ & \quad=\boldsymbol{\Gamma}_{-j}\end{aligned} - 方差
\begin{aligned} \boldsymbol{\Gamma}_0= & E\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)^{\prime} \\ = & \boldsymbol{\Phi}_1E\left(\boldsymbol{Y}_{t-1}-\boldsymbol{\mu}\right)\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)^{\prime}+\boldsymbol{\Phi}_2E\left(\boldsymbol{Y}_{t-2}-\boldsymbol{\mu}\right)\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)^{\prime}+\cdots \\ & +\boldsymbol{\Phi}_p E\left(\boldsymbol{Y}_{t-p}-\boldsymbol{\mu}\right)\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)^{\prime}+E\left[\boldsymbol{\varepsilon}_t\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)^{\prime}\right] \\ = & \boldsymbol{\Phi}_1\boldsymbol{\Gamma}_{-1}+\boldsymbol{\Phi}_2\boldsymbol{\Gamma}_{-2}+\cdots+\boldsymbol{\Phi}_p \boldsymbol{\Gamma}_{-p}+E\left[\boldsymbol{\varepsilon}_t\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)^{\prime}\right]\end{aligned}- 由于
\begin{aligned} E\left[\boldsymbol{\varepsilon}_t\left(\boldsymbol{Y}_t-\boldsymbol{\mu}\right)^{\prime}\right]= & E\left[\boldsymbol{\varepsilon}_t\left(\boldsymbol{Y}_{t-1}-\boldsymbol{\mu}\right)^{\prime}\right] \boldsymbol{\Phi}_1^{\prime}+E\left[\boldsymbol{\varepsilon}_t\left(\boldsymbol{Y}_{t-2}-\boldsymbol{\mu}\right)^{\prime}\right] \boldsymbol{\Phi}_2^{\prime}+\cdots \\ & +E\left[\boldsymbol{\varepsilon}_t\left(\boldsymbol{Y}_{t-p}-\boldsymbol{\mu}\right)^{\prime}\right] \boldsymbol{\Phi}_p^{\prime}+E\left(\boldsymbol{\varepsilon}_t \boldsymbol{\varepsilon}_t^{\prime}\right) \\ = & \mathbf{0}+\mathbf{0}+\cdots+\mathbf{0}+\boldsymbol{\Omega} \\ = & \boldsymbol{\Omega}\end{aligned} - 于是
\begin{aligned} \boldsymbol{\Gamma}_0& =\boldsymbol{\Phi}_1\boldsymbol{\Gamma}_{-1}+\boldsymbol{\Phi}_2\boldsymbol{\Gamma}_{-2}+\cdots+\boldsymbol{\Phi}_p \boldsymbol{\Gamma}_{-p}+\boldsymbol{\Omega} \\ & =\boldsymbol{\Phi}_1\boldsymbol{\Gamma}_1^{\prime}+\boldsymbol{\Phi}_2\boldsymbol{\Gamma}_2^{\prime}+\cdots+\boldsymbol{\Phi}_p \boldsymbol{\Gamma}_p^{\prime}+\boldsymbol{\Omega}\end{aligned}
- 由于
9.1.5 VAR 模型与 VMA 模型的转化
- VMA(q)
\boldsymbol{Y}_t=\boldsymbol{C}+\boldsymbol{\varepsilon}_t+\boldsymbol{\Psi}_1\boldsymbol{\varepsilon}_{t-1}+\boldsymbol{\Psi}_2\boldsymbol{\varepsilon}_{t-2}+\cdots+\boldsymbol{\Psi}_q \boldsymbol{\varepsilon}_{t-q} - VAR(1)模型的转化
\begin{aligned} \boldsymbol{Y}_t & =\left(\boldsymbol{I}_n-\boldsymbol{\Phi} L\right)^{-1}\left(\boldsymbol{C}+\boldsymbol{\varepsilon}_t\right) \\ & =\left(\boldsymbol{I}_n+\boldsymbol{\Phi} L+\boldsymbol{\Phi}^2L^2+\cdots\right)\left(\boldsymbol{C}+\boldsymbol{\varepsilon}_t\right) \\ & =\left(\boldsymbol{I}_n+\boldsymbol{\Phi}+\boldsymbol{\Phi}^2+\cdots\right) \boldsymbol{C}+\boldsymbol{\varepsilon}_t+\boldsymbol{\Phi} \boldsymbol{\varepsilon}_{t-1}+\boldsymbol{\Phi}^2\boldsymbol{\varepsilon}_{t-2}+\cdots \\ & =\boldsymbol{\mu}+\sum_{i=0}^{\infty} \boldsymbol{\Phi}^{i} \boldsymbol{\varepsilon}_{t-i}\end{aligned} - VAR(q)模型的转化
第12章 GARCH 模型
12.1 背景介绍
- 传统模型
- 残差序列具有不变的条件方差(同方差)
- 残差无意义
- 实际:存在异方差
- 出现波动性集群现象
- 残差方差可以衡量风险程度
12.2 ARCH模型
12.2.1 ARCH模型的定义
- 误差项在t时刻的方差依赖t-1时刻
- ARCH(1)模型
\begin{aligned} y_t & =x_t^{\prime} \phi+u_t, u_t \sim N\left(0, \sigma_t^2\right) \\ \sigma_t^2& =E\left(u_t^2\mid u_{t-1}\right)=\alpha_0+\alpha_1u_{t-1}^2\end{aligned}- 条件异方差:方差随时间变化,并且以过去的扰动项信息为变化条件
- ARCH(p)
\begin{aligned} & y_t=x_t^{\prime} \phi+u_t, \quad u_t \sim N\left(0, \sigma_t^2\right) \\ & \begin{aligned} \sigma_t^2& =E\left(u_t^2\mid u_{t-1}, u_{t-2}, \cdots\right) =\alpha_0+\alpha_1u_{t-1}^2+\alpha_2u_{t-2}^2+\cdots+\alpha_p u_{t-p}^2\end{aligned}\end{aligned}- 扰动项不存在序列相关性,条件期望和无条件期望均为0
12.2.2 ARCH模型的属性
- 误差项
u_t^2-\sigma_t^2=\varepsilon_t - 则方差等式可以看成AR(p)模型
u_t^2=\alpha_0+\alpha_1u_{t-1}^2+\alpha_2u_{t-2}^2+\cdots+\alpha_p u_{t-p}^2+\varepsilon_t
12.2.3 ARCH模型的估计与检验
- OLS回归y_t=x_t^{\prime} \phi+u_t得到残差序列\hat{u}_{t}
- 回归\hat{u}_t^2=c+\alpha_1\hat{u}_{t-1}^2+\alpha_2\hat{u}_{t-2}^2+\cdots+\alpha_p \hat{u}_{t-p}^2+\varepsilon_t
- 进行假设检验:原假设H_0: \alpha_1=\alpha_2=\cdots=\alpha_p=0
12.3 GARCH模型
12.3.1 GARCH(1,1)模型的基本定义
- 方差引入自身滞后项
- GARCH(1,1)模型
\begin{aligned} & y_t=x_t^{\prime} \phi+u_t, u_t \sim N\left(0, \sigma_t^2\right) \\ & \sigma_t^2=\alpha_0+\alpha_1u_{t-1}^2+\beta_1\sigma_{t-1}^2\end{aligned} - GARCH(1,1)可以转换为ARCH(∞)
\begin{aligned} & \sigma_t^2=\alpha_0+\alpha_1u_{t-1}^2+\beta_1\sigma_{t-1}^2\\ & \Rightarrow\left(1-\beta_1L\right) \sigma_t^2=\alpha_0+\alpha_1u_{t-1}^2\\ & \Rightarrow \sigma_t^2=\left(1-\beta_1L\right)^{-1}\left(\alpha_0+\alpha_1u_{t-1}^2\right)=\frac{\alpha_0}{1-\beta_1}+\alpha_1u_{t-1}^2+\alpha_1\beta_1u_{t-2}^2+\alpha_1\beta_1^2u_{t-3}^2+\cdots\end{aligned}- 相较于ARCH,滞后期数更少
12.3.2 GARCH(q,p)模型
- 模型
\begin{aligned} & y_t=x_t^{\prime} \phi+u_t, u_t \sim N\left(0, \sigma_t^2\right) \\ & \sigma_t^2=\alpha_0+\sum^p \alpha_i u_{t -i}^2+\sum^q \beta_j \sigma_{t-j}^2\end{aligned} - 使用滞后算子
\beta(L) \sigma_t^2=\alpha_0+\alpha(L) u_t^2- 则
\sigma_t^2=\beta(L)^{-1} \alpha_0+\beta(L)^{-1} \alpha(L) u_t^2 - GARCH(q,p)可以转换为ARCH(∞)
- 则
12.3.3 GARCH 模型的属性
- 由于
u_t^2-\sigma_t^2=\varepsilon_t - 因此
\begin{align} u_t^2-\varepsilon_t=\alpha_0+\sum_{i=1}^p \alpha_i u_{t-i}^2+\sum_{i=1}^q \beta_j\left(u_{t-j}^2-\varepsilon_{t-j}\right) \\ u_t^2=\alpha_0+\sum_{i=1}^m\left(\alpha_i+\beta_i\right) u_{t-i}^2+\varepsilon_t-\sum_{j=1}^q \beta_j \varepsilon_{t-j} \end{align} - 平稳条件:落在单位圆外
1-\left(\alpha_1+\beta_1\right) z-\left(\alpha_2+\beta_2\right) z^2-\cdots-\left(\alpha_m+\beta_m\right) z^m=0 - 均值
E\left(u_t^2\right)=\sigma^2=\frac{\alpha_0}{1-\sum_{i=1}^m\left(\alpha_i+\beta_i\right)}