
第一章 导论
博弈
- 定义:理性人在一定的约束条件下从可选方案中选择最优行动并从中获得收益的过程
- 博弈的要素
- 博弈方:又称参与人
- 行动:博弈方可以采用的行为
- 策略:可供每个博弈方进行选择的所有行动组合。如果把任一博弈方i的行动记为a_i,其策略为S_i,则a_i\in S_i
有时候策略和行动意思相同 - 收益:博弈各方在不同行动组合下的所得
- 信息:博弈方在博弈过程中所知悉的知识,包括博弈的步骤、各方策略、收益。
完全信息:博弈各方对于不同行动组合下的收益是共同知识
共同知识:所有博弈方知道的、所有博弈方知道所有博弈方知道的、所有博弈方知道所有博弈方知道所有博弈方知道的...
简单博弈的描述方法
- 规范式:用收益矩阵描述,需要博弈双方同时采取行动(静态博弈)
- 扩展式:用树来描述,博弈双方存在行动先后顺序(动态博弈)
- 使用虚线表示后行动者不知道先行动者的选择
博弈的分类
- 是否存在先后次序
- 静态博弈:行动同时采取,如剪刀石头布
- 动态博弈:行动有先后次序,如下棋
- 博弈是否重复
- 一次性博弈:如买东西
- 动态博弈:如人与人的关系
- 收益情况
- 零和博弈:双方收益之和为零,如猜硬币
- 常和博弈:双方收益之和为固定值:如双人分钱
- 变和博弈:双方收益之和不固定,如夫妻之争
- 对信息的获悉情况
- 完全/非完全信息:各方对不同行动组合下的各方收益信息是否为共同信息
- 完美/非完美信息:后行动者采取行动时是否知道先行动者的行动选择
- 博弈方数量
- 单人博弈
- 双人博弈
- 多人博弈
第二章 完全信息静态博弈
纯策略纳什均衡
纳什均衡
- 策略组合由博弈各方的最优策略组成
- 纳什均衡下,各方都愿意保持当前行动不变,一旦采取其它行动就会损失自己的收益
- 博弈的纳什均衡
- 给定一方的行动,在另一方的策略中选择最高收益的行动
- 给定另一方选择了前述最高收益的行动,判断前述给定的一方行动是否也为最优
- 如果符合,该行动组合就是纳什均衡,因为任何一方更改行动都会损失收益
- 纳什均衡可能有多个
- 纳什均衡不一定是对总体最好的
上策均衡
- 上策又称占优策略。不管其它博弈方采取何种行动,如果某一行动带来的收益总是超过其它行动,那么该行动是占优策略
- 如果行动组合对所有参与者都是上策,那么该行动组合是纳什均衡
- 上策均衡一定是纳什均衡,纳什均衡不一定是上策均衡;如果上策均衡存在则纳什均衡唯一
劣策略
- 严格劣策略
- 对于博弈方i,对于其它博弈方的任意策略,若策略s_i带来的收益总是小于其它策略,则s_i是i的严格劣策略
- 严格劣策略不会被博弈方采取,因此可以剔除,直至所有博弈方都没有严格劣策略
- 反复剔除严格劣策略不会剔除纳什均衡
- 弱劣策略
- 对于博弈方i,对于其它博弈方的任意策略,存在策略s_j使策略s_i带来的收益总是小于除策略s_j外的其它策略、等于策略s_j,则s_i是i相对于策略s_j的弱劣策略
- 反复剔除弱劣势策略可能剔除纳什均衡,且与剔除顺序有关
帕累托最优结果
- 帕累托最优
- 资源配置状态已经达到除非损害一些人利益才能使得另一些人状况改善
- 帕累托改进
- 可以在不损害任何一方的利益情况下使得某些人情况变好
- 帕累托占优
- 若行动组合A给所有博弈方带来的收益大于等于行动组合B,则A帕累托占优B
混合策略纳什均衡
混合策略
- 任何一方不会固定采取某个策略,而是给每个策略分配有关概率
混合策略纳什均衡
- 计算方法:
- 方法一:在给定各方混合策略的情况下各方最大化自己的期望收益
- 方法二:任一博弈方的最优混合策略必须使对方选择不同策略的期望收益相等
- 如猜硬币,盖硬币方选择正面的概率为r,猜硬币方猜正面概率为q
- 方法一:盖硬币方期望收益[q \times(-1)+(1-q) \times1]+(1-r)[q \times1+(1-q) \times(-1)],对r求偏导等于0得q=\frac{1}{2}
- 方法二:盖硬币方的收益与猜硬币方策略无关,r \times1+(1-r) \times(-1)=r \times(-1)+(1-r) \times1,得到r=\frac{1}{2}
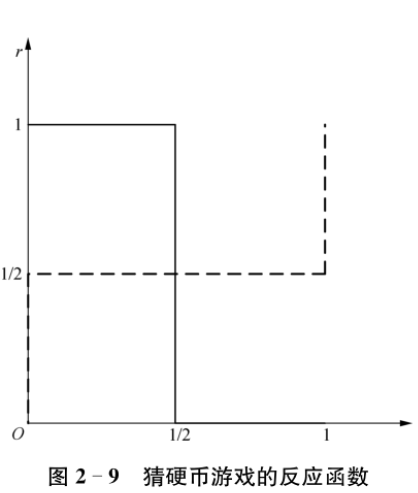
混合策略下的反应函数
- 自变量为自己的混合策略,因变量为对方的混合策略
- 通过分析自己不同混合策略下对方的收益从而判断对方的混合策略,得到反应函数
- 下图表示
- 当猜硬币方猜正面概率小于0.5时,盖硬币方一定会选择正面;当猜硬币方猜正面概率大于0.5时,盖硬币方一定会选择反面
- 当盖硬币方选择正面概率小于0.5时,猜硬币方一定会猜反面;当盖硬币方选择正面概率大于0.5时,猜硬币方一定会猜正面
反复剔除严格劣于混合策略的纯策略
- 当策略的行动数量超过两个时,混合策略的某个行动的概率可能不在0到1之间,此时说明出现了严格劣于混合策略的纯策略
- 在一个完全信息静态博弈中,如果某个博弈方的某个策略给其带来的收益小于其他策略的某个混合策略给他带来的期望收益,那么我们说该策略是其他策略的某个混合策略的严格劣策略。此时,该策略可以从该博弈中剔除掉
- 剔除说明该行动的概率为0,避免了概率范围超出0到1
纳什定理:如果一个博弈有有限个博弈方,每个博弈方的策略也是有限的,那么,该博弈一定存在纳什均衡,其中可能包括混合策略纳什均衡。
一些拓展
帕累托上策均衡和风险上策均衡
- 在多重纯策略纳什均衡中,给博弈双方带来的总收益更高的纳什均衡为帕累托上策均衡
- 给定一方采取如下混合策略,即以相同的概率选择两个不同的行动,给另一方带来期望收益更高的行动将被选择。各博弈方采取的行动构成的纳什均衡即为风险上策均衡
聚点均衡和相关均衡
- 够让博弈双方“想到一块”的信息相当于一个聚点,为双方所选择。这样形成的纳什均衡为聚点均衡
- 博弈双方基于一些共同的信号进行策略选择,以使博弈双方以一定的概率选择总收益最高的策略组合
防共谋均衡
- 在完全信息静态博弈的环境下,利益可能因其他博弈方合谋而受损的博弈方也会认识到这种可能,从而选择不给其他博弈方采取合谋机会的策略。这种不给多人博弈中部分博弈方合谋机会的纳什均衡,我们称之为防共谋均衡。
第三章 完全完美信息动态博弈
完全且完美信息动态博弈
基本概念
- 动态博弈:博弈方行动存在先后顺序
- 完全信息:关于收益的知识为共同知识
- 完美信息:后行动者知道此前行动者的行动选择
博弈方的纯策略
- 指博弈方在其采取行动的所有阶段的一套完整的行动方案,亦即博弈方在其采取行动的每个决策节下的所有行动方案
- 如囚徒困境中,第一个人的纯策略是“坦白”和“抗拒”,第二个人的纯策略是“坦白-抗拒”、“抗拒-抗拒”、“坦白-坦白”和“抗拒-坦白”
纯策略纳什均衡
- 画出规范式
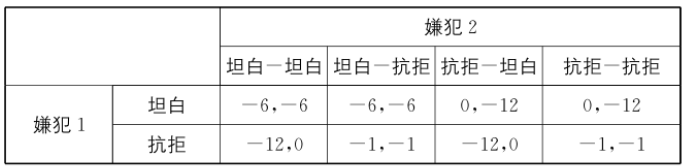
- 完全且完美信息动态博弈可以转化为规范式表述的静态博弈,且该静态博弈的纯策略纳什均衡也是该完全且完美信息动态博3. 一个规范式表述的静态博弈并不能转化成完全且完美信息动态博弈,因为同一个静态博弈可以转换为多种形式的动态博弈。
子博弈完美纳什均衡
可信性问题
- 问题:部分纳什均衡并不稳定,缺乏一致性预测的能力。
- 即策略之间存在约束关系导致某些策略无法达成,有前后依赖关系
- 使用逆推法可以正确求解纳什均衡
逆推法
- 从最后一个阶段依次向前分析
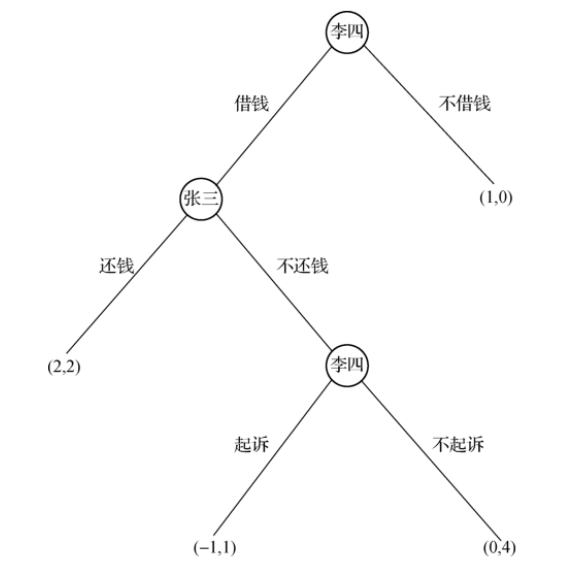
- 以下图为例
- 最后一个阶段,李四会选择起诉
- 第二个阶段,由于李四会起诉,张三会选择还钱
- 第一阶段,由于借钱收益为2,李四会选择借钱
子博弈完美纳什均衡
- 子博弈:指始于某个动态博弈的某个独立决策节以后且能够自成一个独立博弈的部分。一个子博弈开始的决策节必须有独立的信息集(行动收益不受之前的博弈影响),此后阶段决策节的信息集可以不独立,但是必须存在于该子博弈之内
- 子博弈完美纳什均衡:策略组合不仅在整个完美信息动态博弈中构成纳什均衡,也在该动态博弈的所有子博弈中构成纳什均衡