第二章 流密码
流密码的基本概念
- 密钥k通过密钥流发生器z_i=f(k,\sigma_i)产生密钥流 \mathbf{z}=z_0z_1\dots,\sigma_i为i时刻的状态
- 通过密钥流,加密 \mathbf{x}=x_0x_1\dots,得到密文 \mathbf{y}=y_0y_1\dots=E_{z_0}(x_0)E_{z_1}(x_1)\dots
- 解密时\mathbf{x}=x_0x_1\dots=D_{z_0}(y_0)D_{z_1}(y_1)\dots,D_{z_i}是E_{z_i}的逆运算
流密码的分类
- 同步流密码
- \sigma_i独立于明文流,即密钥流的生成与明文流无关
- 可以先产生密钥流,再加密。因为密钥流生成不依赖明文流
- 自同步密码
- \sigma_i与明文流有关,密钥流的生成依赖已输入的明文
- 只能一边生成密钥流,一边加密,以此往复。因为只有获取了上一时刻的明文,才能生成下一时刻的密钥
- 由于自同步流密码的密钥流的产生与明文有关,因而较难从理论上进行分析
同步流密码
- 同步流密码的加密器分成密钥流产生器和加密变换器两个部分
- 加密变换E_{z_i}可以有多种选择,只要变换是可逆的即可
- 加法流密码:最常使用同步流密码,加密变换和解密运算都是的是异或运算,即y_i=E_{z_i}(x_i)=z_i\oplus x_i、x_i=D_{z_i}(y_i)=z_i\oplus y_i
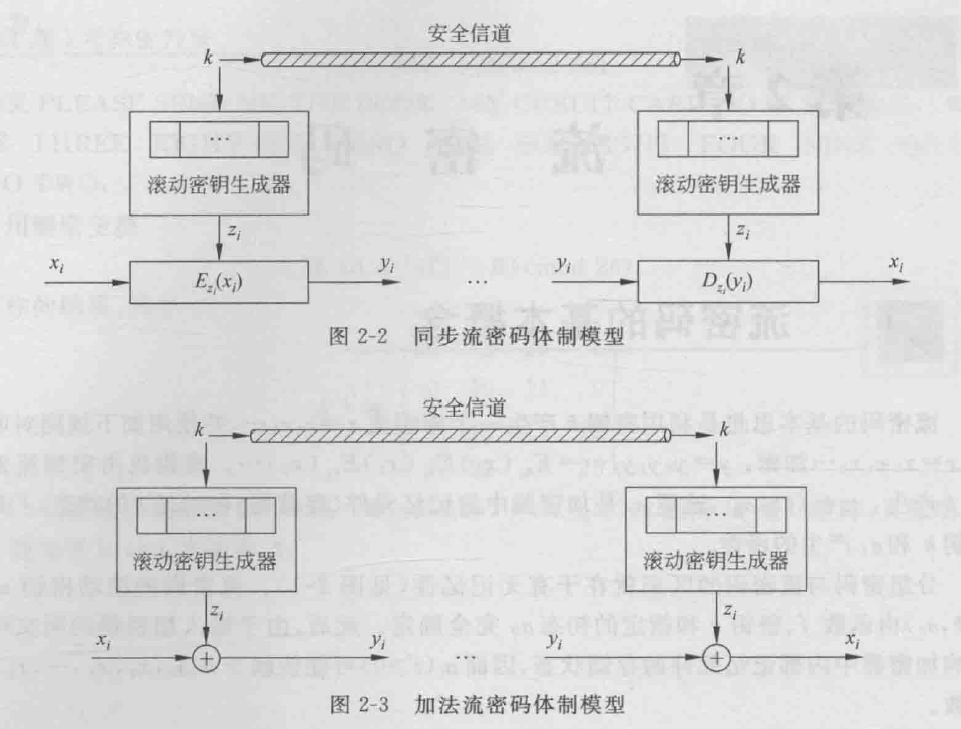
- 同步流密码应当满足:极大的周期、良好的统计特性、抗线性分析、抗统计分析.
有限状态自动机
- 有限状态自动机是具有离散输入和输出(输入集和输出集均有限)的一种数学模型,由以下3部分组成
- 有限状态集\mathbf{S}=\left\{s_i \mid i=1,2, \cdots, l\right\}
- 有限输入字符集\mathbf{A}_1=\left\{A_j^{(1)} \mid j=1,2, \cdots, m\right\}和有限输出字符集\mathbf{A}_2=\left\{A_k^{(2)} \mid k=1\right.,2, \cdots, n\}
- 转移函数A_k^{(2)}=f_1\left(s_i, A_j^{(1)}\right), s_h=f_2\left(s_i, A_j^{(1)}\right)
- 即自动机的状态为s_i时,从有限输入字符集\mathbf{A}_1选择一个字符A_j^{(1)}输入到自动机,可以得到有限输出字符集\mathbf{A}_2中某一字符A_k^{(2)},同时自动机的状态更新为s_h
密钥流产生器
- 同步密码流通过密钥和密钥流产生器产生密钥流
- 密钥流产生器的结构
- 输入的密钥k
- 初始状态\sigma_0
- 状态转移函数\sigma_{i+1}=\varphi (\sigma_i,k)
- 输出函数z_i=\psi (\sigma_i,k)
- 密钥流产生器是有限状态自动机,包含
- 有限状态集\mathbf{S}=\{\sigma_0,\sigma_1,\dots\}
- 有限输入字符集\mathbf{A}_1=\{k\}
- 有限输出字符集\mathbf{A}_2=\{z_0,z_1,\dots\}
- 转移函数f_1=\psi、f_2=\varphi
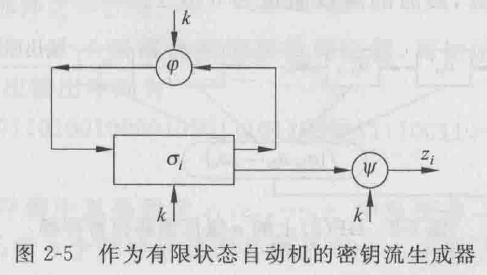
- 关键在于找出适当的状态转移函数和输出函数,即满足同步流密码的需求,并且容易实现,因此必须有非线性函数
- 具有非线性f_2的有限状态自动机理论很不完善,因此密钥流产生器的f_2即状态转移函数往往为线性,f_1即输出函数往往为非线性
线性反馈位移寄存器LFSR
- 移位寄存器是流密码产生密钥流的一个主要组成部分
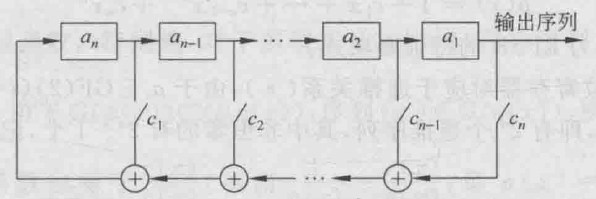
- n级反馈位移寄存器由n个二元存储器组成,记为\{a_n,a_{n-1},\dots,a_1\};同时有反馈函数f\left(a_1, a_2, \cdots, a_n\right),值域为\{0,1\}
- 二元存储器可以为0或1,所以有限状态集\mathbf{S}包含2^n中状态
- 有限输入字符集\mathbf{A}_1=\emptyset,即输出只依赖初始状态,不需要输入
- 有限输出字符集\mathbf{A}_2=\{0,1\},输出是0或1
- 转移函数f_1,将a_1存储器的数值数输出
- 转移函数f_2,首先计算a=f\left(a_1, a_2, \cdots, a_n\right),然后将a_i赋值为a_{i+1}的值(i=1,2,\dots,n-1),最后将a_n赋值为a
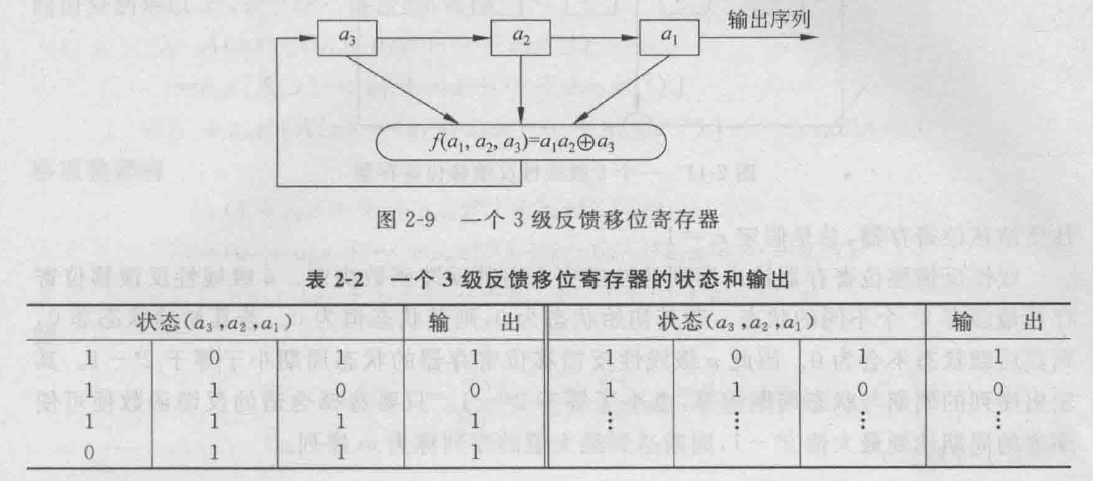
- 如果反馈函数f\left(a_1, a_2, \cdots, a_n\right)是线性函数,即f可写为
f\left(a_1, a_2, \cdots, a_n\right)=c_n a_1\oplus c_{n-1} a_2\oplus \cdots \oplus c_1a_n\quad (c_i=0,1)
则称之为线性反馈移位寄存器(Linear Feedback Shift Register,LFSR),c_i=0或1可以用开关的断开和闭合实现
- LFSR的性质由初始状态和反馈函数决定
- 初始状态为全0,其后继状态恒为全0;初始状态不为全0,其后继状态不会为全0
- 状态周期与输出序列周期相等,小于等于2^n-1
- 周期为2^n-1的LFSR输出的序列被称为m序列
线性移位寄存器的一元多项式表示
- 特征多项式
- 由
a_{n+1}=c_n a_1\oplus c_{n-1} a_2\oplus \cdots \oplus c_1a_n
可得
a_{n+k}=c_1a_{n+k-1} \oplus c_2a_{n+k-2} \oplus \cdots \oplus c_n a_k
这种递推关系可以用一个一元高次多项式表示
p(x)=1+c_1x+\cdots+c_{n-1} x^{n-1}+c_n x^n
这个多项式为LFSR的特征多项式 - 显然p(x)有2^n种情况,能产生2^n-1个非恒零的输出序列\{a_i\},记为\mathbf{G}(p(x))
- 对于输出序列\{a_i\},幂级数
A(x)=\sum_{i=1}^{\infty} a_i x^{i-1}
称为该序列的生成函数
- 由
- 性质
- 性质一
p(x) A(x) =\sum_{i=1}^n\left(c_{n-i} x^{n-i} \sum_{j=1}^i a_j x^{j-1}\right)=\phi (x) \\ = \left(a_1+a_2x+\cdots+a_n x^{n-1}\right)+c_1x\left(a_1+a_2x+\cdots+a_{n-1} x^{n-2}\right) +c_2x^2\left(a_1+a_2x+\cdots+a_{n-2} x^{n-3}\right)+\cdots+c_{n-1} x^{n-1} a_1 - 性质二
p(x) \mid q(x)的充要条件是\mathbf{G}(p(x)) \subset \mathbf{G}(q(x))。
上述定理说明可用n级LFSR产生的序列,也可用级数更多的LFSR来产生 - 性质三
使p(x) \mid (x^n-1)成立的最小n称为p(x)的周期或阶。则\{a_i\}的周期r \mid n - 性质四
若p(x)是不可约多项式,周期为m,输出序列\{a_i\}\in \mathbf{G}(p(x)),则输出序列\{a_i\}的周期为m
即不可约多项式p(x)的2^n-1个非恒0输出序列具有相同周期,等于不可约多项式的周期 - 性质五
n级LFSR产生的序列有最大周期2^n-1的必要条件是其特征多项式为不可约多项式
反过来不成立 - 性质六
若不可约多项式p(x)的阶为2^n-1,则称为本原多项式。\{a_i\}是m序列的充要条件是p(x)为本原多项式 - 性质七
n次本原多项式的个数为\frac{\varphi\left(2^n-1\right)}{n},所以对于任意的n级LFSR,至少存在一种连接方式使其输出序列为m序列.
- 性质一
m序列密码的破译
假设知道一段长为2n的明密文对
x=x_1x_2\cdots x_{2n}, \quad y=y_1y_2\cdots y_{2n}
异或运算后求出一段长为2n的密钥对
z=z_1z_2\cdots z_{2n}
于是可以求出LFSR的连续n+1个状态
\begin{aligned} & \boldsymbol{S}_1=\left(z_1z_2\cdots z_n\right) \stackrel{\text {记为}}{=}\left(a_1a_2\cdots a_n\right) \\ & \boldsymbol{S}_2=\left(z_2z_3\cdots z_{n+1}\right) \stackrel{\text {记为}}{=}\left(a_2a_3\cdots a_{n+1}\right) \\ & \vdots \\ & \boldsymbol{S}_{n+1}=\left(z_{n+1} z_{n+2} \cdots z_{2n}\right) \stackrel{\text {记为}}{=}\left(a_{n+1} a_{n+2} \cdots a_{2n}\right)\end{aligned}
设矩阵
\boldsymbol{X}=\left(\boldsymbol{S}_1\boldsymbol{S}_2\cdots \boldsymbol{S}_n\right)
则
\begin{aligned}\left(a_{n+1} a_{n+2} \cdots a_{2n}\right) & =\left(c_n c_{n-1} \cdots c_1\right)\left(\begin{array}{ccc}a_1& \cdots & a_n \\ \vdots & & \vdots \\ a_n & \cdots & a_{2n-1}\end{array}\right) \\ & =\left(c_n c_{n-1} \cdots c_1\right) \mathbf{X}\end{aligned}\\ \left(c_n c_{n-1} \cdots c_1\right)=\left(a_{n+1} a_{n+2} \cdots a_{2n}\right) \mathbf{X}^{-1}
非线性序列
- LFSR使用了线性f_2,安全性不足,因此可以通过对多个LFSR的非线性组合,构造非线性序列
- 基本原则
- 长周期
- 高线性复杂度
- 统计性能良好
- 足够的"混乱"
- 足够的"扩散"
- 抵抗不同形式的攻击
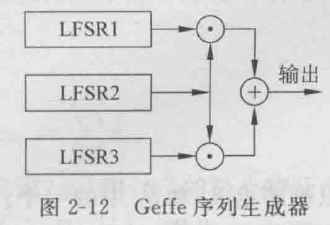
- Geffe序列生成器
- 由3个LFSR组成,每个LFSR都为本原多项式,且两两互素。其中LFSR2作为控制生成器使用,选择输出LFSR1还是LFSR3的结果
- 周期为T=\prod_{i=1}^3\left(2^{n_i}-1\right),实现了周期的最大化
- 线性复杂度为\delta=\left(n_1+n_3\right) n_2+n_3
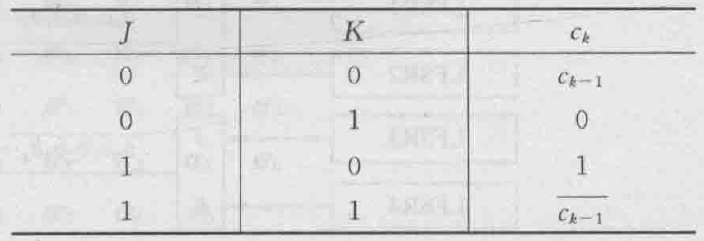
- JK触发器
- 有两个输入端,输出不仅依赖输入端,还和上一个输出有关c_k=\overline{\left(x_1+x_2\right)} c_{k-1}+x_1
- 输入端可以使用LSFR。令驱动序列\left\{a_k\right\}和\left\{b_k\right\}分别为m级和n级m序列,则有c_k=\overline{\left(a_k+b_k\right)} c_{k-1}+a_k=\left(a_k+b_k+1\right) c_{k-1}+a_k
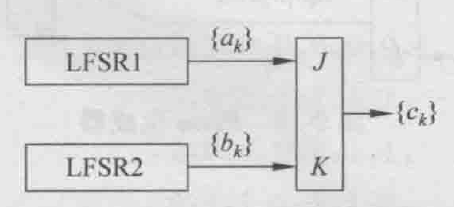
- 当m与n互素且a_0+b_0=1时,序列\left\{c_k\right\}的周期为\left(2^m-1\right)\left(2^n-1\right)。
- Pless生成器
- Pless生成器由8个LFSR、4个JK触发器和1个循环计数器构成,由循环计数器进行选通控制,如图2-16所示.假定在时刻t输出第t(mod4)个单元,则输出序列为
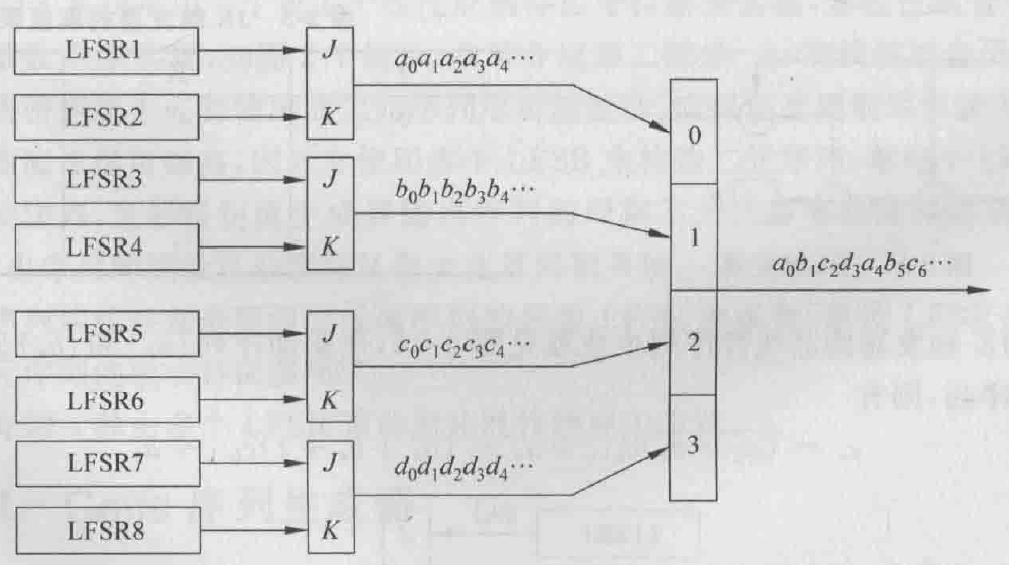
- 钟控序列生成器
- 用LFSR1控制LFSR2的移位时钟脉冲,若控制LFSR1输出0,则LFSR2输出与上一时刻相同

- 周期
p=\frac{p_1p_2}{\operatorname{gcd}\left(w_1, p_2\right)},w_1=\sum_{i=0}^{p_1-1} a_i
第三章 分组密码体制
分组密码概述
- 分组密码是将明文消息编码表示后的数字序列x_0, x_1, \cdots, x_i, \cdots划分成长为n的组\boldsymbol{x}=\left(x_0, x_1, \cdots, x_{n-1}\right),各组(长为n的矢量)分别在密钥\boldsymbol{k}=\left(k_0, k_1, \cdots, k_{t-1}\right)控制下变换成等长的输出数字序列\boldsymbol{y}=\left(y_0, y_1, \cdots, y_{m-1}\right) (长为m的矢量),其加密函数E: V_n \times K \rightarrow V_m, V_n和V_m分别是n维和m维矢量空间, K为密钥空间
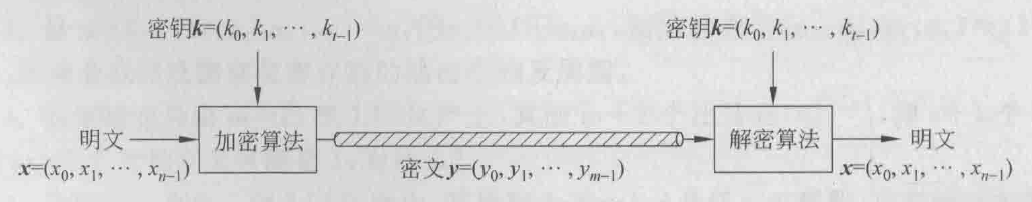
- 通常取m=n 。若m\gt n,则为有数据扩展的分组密码。若m\lt n,则为有数据压缩的分组密码。
- 在二元情况下, \boldsymbol{x}和\boldsymbol{y}均为二元数字序列,它们的每个分量x_i, y_i \in \mathrm{GF}(2) 。下面主要讨论二元情况。设计的算法应满足下述要求:
- 分组长度n要足够大,使分组代换字母表中的元素个数2"足够大,防止明文穷举攻击法奏效
- 密钥量要足够大(即置换子集中的元素足够多),尽可能消除弱密钥并使所有密钥同等地好,以防止密钥穷举攻击奏效;但密钥又不能过长,以便于密钥的管理
- 由密钥确定置换的算法要足够复杂,充分实现明文与密钥的扩散和混淆,没有简单的关系可循,能抗击各种已知的攻击,如差分攻击和线性攻击;有高的非线性阶数,实现复杂的密码变换;使对手破译时除了用穷举法外,无其他捷径可循。
- 加密和解密运算简单,易于软件和硬件高速实现;加密和解密过程之间的差别应仅在于由秘密密钥所生成的密钥表不同而已。这样,加密和解密就可使用同一器件实现。
- 数据扩展尽可能小。一般无数据扩展,在采用同态置换和随机化加密技术时可引入数据扩展。
- 差错传播尽可能小。
代换
- 为使加密运算可逆(使解密运算可行),明文的每一个分组都应产生唯一的一个密文分组,这样的变换是可逆的,称明文分组到密文分组的可逆变换为代换。
- 如果分组长度太小,系统则等价于古典的代换密码,容易通过对明文的统计分析而攻破。如果分组长度n足够大,而且从明文到密文可有任意可逆的代换,那么明文的统计特性将被隐藏而使以上的攻击不能奏效。
- 从实现的角度来看,分组长度很大的可逆代换结构是不实际的。对n比特的代换结构,密钥的大小是n \times2^n比特。
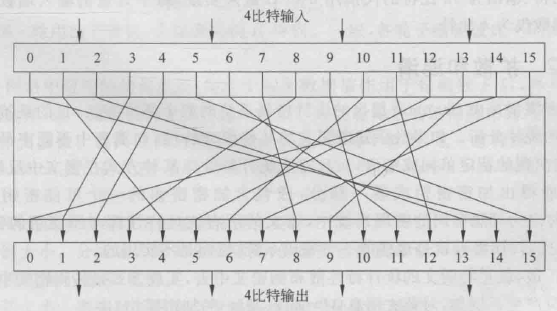
扩散和混淆
- 扩散和混淆是由 Shannon提出的设计密码系统的两个基本方法,目的是抗击敌手对密码系统的统计分析。理想情况下密文的所有统计特性都与所使用的密钥独立
- 扩散是将明文的统计特性散布到密文中去,实现方式是使得密文中每一位由明文中多位产生。在二元分组密码中,可对数据重复执行某个置换再对这一置换作用以一个函数,便可获得扩散。
- 扩散的目的是使明文和密文之间的统计关系变得尽可能复杂,以使敌手无法得到密钥
- 混淆是一种使密钥与密文之间的关系尽可能模糊的加密操作。如今实现混淆常用的一个元素就是替换
- 混淆是使密文和密钥之间的统计关系变得尽可能复杂,以使敌手无法得到密钥。
- 使用复杂的代换算法可得预期的混淆效果,而简单的线性代换函数得到的混淆效果不够理想。
Feistel密码结构
- Feistel提出利用乘积密码可获得简单的代换密码,乘积密码指顺序地执行两个或多个基本密码系统,包括多次扩散和混淆等
- Feistel加密结构
- 加密算法输人长为2w的明文和一个密钥K。将明文分成左右两半L_0和R_0,在进行完n轮迭代后,左右两半再合并到一起以产生密文分组。其第i轮迭代的输人为前轮输出的函数:\begin{aligned}& L_i=R_{i-1} \\& R_i=L_{i-1} \oplus F\left(R_{i-1}, K_i\right)\end{aligned} - 其中K_i是第i轮用的子密钥,由加密密钥K得到。一般,各轮子密钥彼此不同而且与K也不同。
- Feistel网络的实现与以下参数和特性有关
分组大小
密钥大小
轮数
子密钥产生算法
轮函数 - 在设计Feistel 网络时,还要考虑以下两个问题:
快速的软件实现
算法容易分析
- Feistel 解密结构
- Feistel解密过程本质上和加密过程是一样的,算法使用密文作为输人,但使用子密钥K_i的次序与加密过程相反,即第一轮使用K_n,第二轮使用K_{n-1},一直下去,最后一轮使用K_1。这一特性保证了解密和加密可采用同一算法。
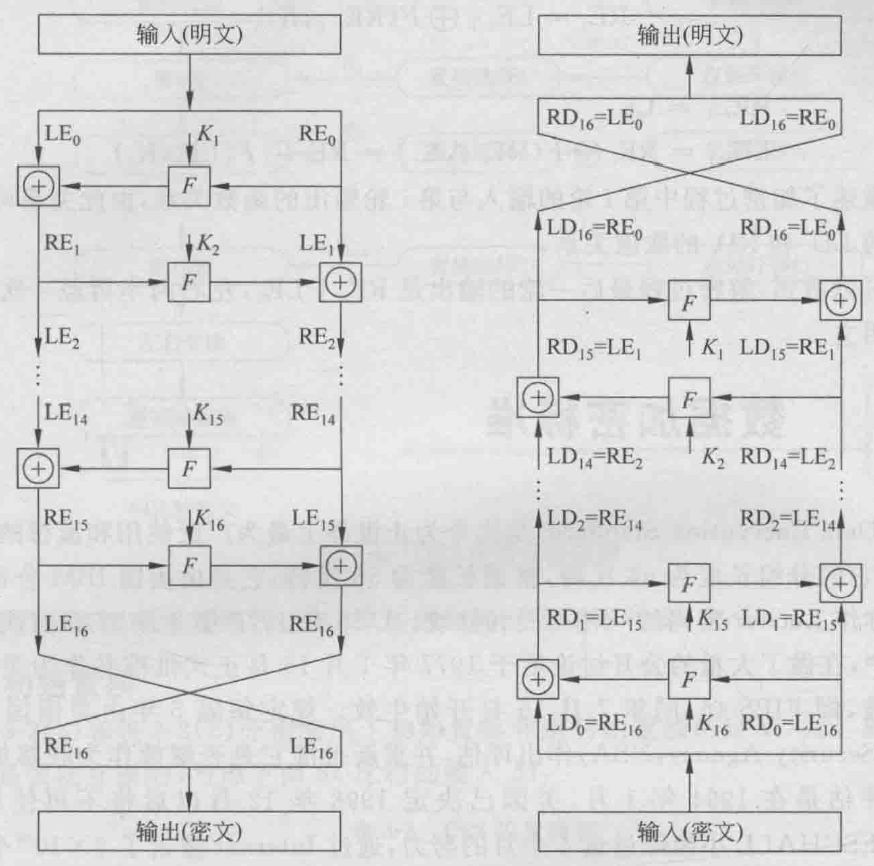
- Feistel解密过程本质上和加密过程是一样的,算法使用密文作为输人,但使用子密钥K_i的次序与加密过程相反,即第一轮使用K_n,第二轮使用K_{n-1},一直下去,最后一轮使用K_1。这一特性保证了解密和加密可采用同一算法。
数据加密标准
DES描述

- 生成16个子秘钥
- 输入64位的秘钥K
- 根据PC1盒,将64位秘钥压缩映射为56位的K_{raw}(丢弃了K的第8,16,24,32,40,48,56,64位的数据)
- 根据LOOP盒,连续左移K_{raw}16次,得到K_{raw,i}\quad i=1,2,\cdots,16
- 根据PC2盒,将K_{raw,i}压缩映射为48位的K_i\quad i=1,2,\cdots,16(丢弃了K_{raw,i}的第9,18,27,36,45,54位的数据)
- K_i\quad i=1,2,\cdots,16就是16个子秘钥
- 初始置换
- 根据IP盒将64位输入打乱得到64位输出
- 轮结构,共分16轮,以第i轮为例
- 将输入拆分为L,R,各32位
- 使用E盒将R扩展映射为48位的R_E(重复使用了R的第1, 4, 5, 8, 9, 12, 13, 16, 17, 20, 21, 24, 25, 28, 29, 32位的数据)
- R_E与K_i异或运算得到R_{E,K}
- 将R_{E,K}每6位分成8组,对于第i组,取1,6位合并得到的二进制数为row、2,,3,4,5位合并得到的二进制数为col,得到S_i=S[i][col][row],拼接8个S_i,得到32位的R_{E,K,S}
- 使用P盒将R_{E,K,S}打乱得到32位的R_{E,K,S,P}
- 拼接R_{E,K,S,P}和L,得到64位的输出
- 最终置换
- 将重复16次轮结构的输出O拆分为L,R,各32位,调换L,R的位置得到O'
- 利用IP^{-1}盒打乱O',输出即为密文
- 由于是Feistel 密码,解密时采用同一算法,但子密钥使用的顺序相反
二重DES
- 秘钥112位,拆分成两个56位秘钥使用
- 加密C=E_{K_2}\left[E_{K_1}[P]\right]
- 解密P=D_{K_1}\left[D_{K_2}[C]\right]
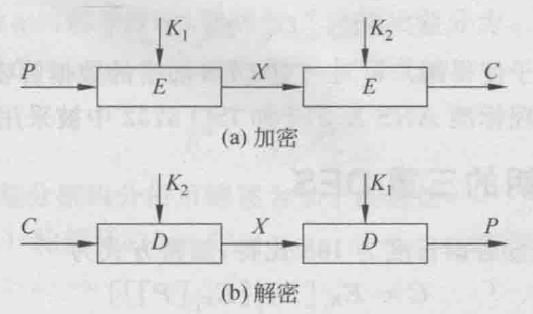
- 二重DES无法简化成一重DES,二重DES的明文密文映射范围大于一重DES
- 中途相遇攻击
- 已知至少2个明文密文对时
- X=E_{K_1}[P]=D_{K_2}[C],用2^{56}个秘钥分别加密P、解密C,得到两张表
- 如果两张表有重复的X,则对应的两个秘钥就可能是K_1,K_2,用另一个明文密文对验证即可判断
- 已知两个明文密文对时,找到正确秘钥的概率为1-2^{-16}
两个密钥的三重 DES
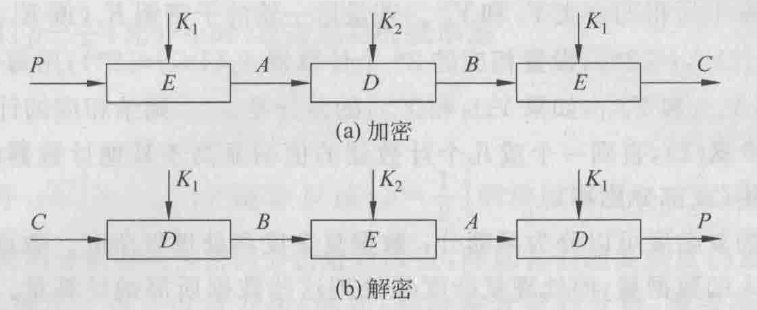
- 秘钥112位,拆分成两个56位秘钥使用。EDE模式下
- 加密C=E_{K_1}\left[D_{K_2}\left[E_{K_1}[P]\right]\right]
- 解密P=D_{K_1}\left[E_{K_2}\left[D_{K_1}[C]\right]\right]
三个密钥的三重DES
- 秘钥168位,拆分成三个56位秘钥使用