信息安全数学基础 | 一个好名字

第1章整数的可除性

整除的概念

设 $a,b$ 是任意两个整数，其中 $b\ne 0$ 。如果存在一个整数 $q$ 使得等式
$a=qb$
成立，就称 $b$ 整除 $a$ 或者 $a$ 被 $b$ 整除，记作 $b|a$ ，并把 $b$ 叫做 $a$ 的因数，把 $a$ 叫做 $b$ 的倍数

$b|a,c|b\Rightarrow c|a$
$c|a,c|b\Rightarrow c|(sa+tb)$
$a|b,b|a\Rightarrow a=\pm b$

素数

除 $\pm 1,\pm n$ 外没有其它因数的 $n$

设 $n$ 是一个正合数， $p$ 是一个大于1的最小正因数，则 $p$ 一定是素数，且 $p\le\sqrt n$
设 $n$ 是正整数。如果对所有的素数 $p\le\sqrt n$ ，都有 $p\nmid n$ ，则 $n$ 一定是素数

欧几里得除法

辗转相除

第8章群

定义

设 $G$ 是一个具有结合法的非空集合，如果 $G$ 中的结合法满足以下三个条件,则G叫做一个群

封闭性
结合律
即对任意的 $a,b,c\in G$ ，都有 $(ab)c=a(bc)$
单位元
即存在一个元素 $e\in G$ ，使得对任意的 $a\in G$ ，都有 $ae=ea=a$
加法群的单位元也叫零元
可逆性
即对任意的 $a\in G$ ，都存在 $a^{-1}\in G$ ，使得 $aa^{-1}=a^{-1}a=e$
加法群的逆元也叫负元

群元素的阶

群 $G$ 的元素个数叫做群 $G$ 的阶，记为 $\left |G \right |$
如果 $\left |G \right |\lt + \infty$ ， $G$ 叫做有限群，否则 $G$ 叫做无限群

交换群

如果群G中的结合法还满足交换律
即对任意的 $a,b\in G$ ，都有 $ab=ba$
那么， $G$ 叫做一个交换群或阿倍尔（Abel）群

群的一些性质

单位元唯一
逆元唯一
$(a_1a_2\dots a_n)^{-1}=a_n^{-1}\dots a_2^{-1}a_1^{-1}$
$a_1a_2\dots a_n$ 的结果不受其排列位置和结合方式的影响
$a^ma^n=a^{m+n},(a^m)^n=a^{mn}$
当 $x,y \in G$ ， $G$ 为阿贝尔群，则 $(xy)^n=x^ny^n$

子群

设 $H$ 是群 $G$ 的一个子集合。如果对于群 $G$ 的结合法， $H$ 成为一个群，那么 $H$ 就叫做群 $G$ 的子群，记作 $H\le G$
$H={e}$ 和 $H=G$ 都是群 $G$ 的子群，叫做群 $G$ 的平凡子群；
如果群 $G$ 的子群 $H$ 不是群 $G$ 的平凡子群，群 $H$ 叫做群 $G$ 的真子群。

子群的证明

群 $G$ 的非空子集 $H$ 是群 $G$ 的子群当且仅当

$H$ 满足 $G$ 下的封闭二元运算
$G$ 的单位元在集合 $H$ 内
对于所有 $a\in H$ 满足 $a^{-1}\in H$

或，对任意 $a,b\in H$ ，有 $ab^{-1}\in H$

子群的交集一定是子群，子群的并集不一定是子群

子群的生成

设 $G$ 是一个群， $X$ 是 $G$ 的子集。设 $\{H_i\}_{i\in I}$ 是 $G$ 的包含 $X$ 的所有子群，则 $\bigcap_{i\in I}H_i$ 叫做 $G$ 的由 $X$ 生成的子群，记为 $\langle X \rangle$

$X$ 的元素称为子群 $\langle X \rangle$ 的生成元
如果 $X=\left\langle a_1,\dots,a_n \right\rangle$ ，则记 $\langle X \rangle$ 为 $\left\langle a_1,\dots,a_n \right\rangle$
如果 $G=\langle a_1,\dots,a_n \rangle$ ，则称 $G$ 为有限生成的
特别的，如果 $G=\langle a \rangle$ ，则称 $G$ 为 $a$ 生成的循环群

例
由 $\langle 1 \rangle$ 生成 $(Z,+):\{\dots,-2,-1,0,1,2,\dots\}$
由 $\langle 2 \rangle$ 生成 $(2Z,+):\{\dots,-4,-2,0,2,4,\dots\}$

设 $G$ 是一个交换群， $X=\{ a_1,a_2,\dots,a_t\}$ 是 $G$ 的子集，则

当 $G$ 是乘法群
$\langle X\rangle=\{a_1^{n_1}\dots a_t^{n_t}|a_i\in X,n_i\in Z,1\le i\le t\}$
特别的，对任意 $a\in G$ ，有 $\langle a\rangle=\{a^n|n\in Z\}$
当 $G$ 是加法群
$\langle X\rangle=\{n_1a_1+\dots+n_ta_t|a_i\in X,n_i\in Z,1\le i\le t\}$
特别的，对任意 $a\in G$ ，有 $\langle a\rangle=\{na|n\in Z\}$

陪集

设 $H$ 是群 $G$ 的子群， $a$ 是 $G$ 中任意元，
那么
$aH=\{ah|h\in H\}\\ Ha=\{ha|h\in H\}$
分别叫做 $G$ 中 $H$ 的左右陪集
若左右陪集相等，可记为 $[a]_H$ （为避免公式混乱，后面也用这种写法表示左右陪集）
$[a]_H$ 中的元素叫做 $[a]_H$ 的代表元

$a\in [a]_H$

$H=[e]_H$ （平凡陪集）

$a\in H\Leftrightarrow [a]_H=H$

$[a]_H=[b]_H\Leftrightarrow a^{-1}b\in H$

$a^{-1}b\notin H\Leftrightarrow [a]_H\cap [b]_H=\emptyset$

满足 $a^{-1}b$ 相同则为同一个陪集， $b\equiv a(mod\quad H)$

$G=\bigcup_{i\in I}a_iH$

拉格朗日定理

设 $H$ 是群 $G$ 的子群，则
$|G|=[G:H]|H|$
更进一步，如果 $K,H$ 是群 $G$ 的子群，且 $K$ 是群 $H$ 的子群，则
$[G:K]=[G:H][H:K]$

商集

设 $H$ 是群 $G$ 的子群，则 $H$ 在 $G$ 中不同左（右）陪集组成的新集合
$\{[a]_H|a\in G\}$
叫做 $H$ 在 $G$ 中的商集，记作 $G/H$
$G/H=\{[a]_H|a\in G\}=\{[a_i]_H|i\in I\}$
$G/H$ 中不同左（右）陪集的个数叫做 $H$ 在 $G$ 中的指标，记为 $[G:H]$

正规子群

设 $N$ 是群 $G$ 的子群，则对任意 $a\in G$ 以下条件是等价的
$aN=Na\text{(左右陪集相等)}\\ aNa^{-1}=N\\ aNa^{-1}\subset N\text{ 其中 }aNa^{-1}=\{ana^{-1}|n\in N\}$
若子群 $N$ 满足上述条件，则称 $N$ 为群 $G$ 的正规子群

商群

设 $N$ 是群 $(G,\times)$ 的正规子群， $G/H$ 是由 $N$ 在 $G$ 中所有陪集组成的集合，则对于结合法 $\ast$
$[a]_H\ast [b]_H=[a\times b]_H$
$(G/H,\ast)$ 构成一个群，叫做群 $(G,\times)$ 对于正规子群 $N$ 的商群

$Z/nZ=\{\dots,[0]_{nZ},\dots,[n-1]_{nZ},\dots\}=\{[0]_{nZ},\dots,[n-1]_{nZ}\}=\{[0],\dots,[n-1]\}=Z_n$

阿贝尔群

左右陪集相等（注意左右陪集相等不一定是阿贝尔群）
子群都是正规子群
任意子群都可以构造商群
构造的商群也是阿贝尔群

映射关系

令 $f$ 为一个从集合 $A$ 到 $B$ 的映射

$f$ 的像集 $Imf=\{f(a)|a\in A\}$ ，像集是 $B$ 的子集
$f$ 的核集 $Kerf=\{x\in A|f(x)=e'\}$ ， $e'$ 为 $B$ 的单位元，像集是 $A$ 的子集

证明单射
当 $a_1\ne a_2$ 时， $f(a_1)\ne f(a_2)$ 。或者对任意 $f(a_1)=f(a_2)$ 一定有 $a_1=a_2$
证明满射
对于所有 $b\in B$ ，存在 $a\in A$ ，使得 $f(a)=b$

同态

设 $G,G'$ 都是群， $f$ 是 $G$ 到 $G'$ 的一个映射。如果对任意的 $a,b\in G$ ，都有
$f(ab)=f(a)f(b)$
那么， $f$ 叫做 $G$ 到 $G'$ 的一个同态
$f:G\rightarrow G'$

如果 $f$ 是单射，则 $f$ 为单同态
如果 $f$ 是满射，则 $f$ 为满同态
如果 $f$ 是双射，则 $f$ 为同构，记作 $f:G\cong G'$
如果 $G=G'$ ，则 $f$ 为自同态

$Imf=f(G)$ 为同态 $f$ 的像子群
$Kerf=f^{-1}(\{e'\})=\{x\in G|f(x)=e'\}$ 为同态 $f$ 的核子群

证明同构
证明 $f$ 是同态映射
证明 $Kerf={e}$ 或证明 $f$ 是 $G$ 到 $G'$ 的单射
证明 $f$ 是 $G$ 到 $G'$ 满射

特殊映射

嵌入映射（恒等映射）
$f:H\rightarrow G,f(a)=a$
自然映射
$f:G\rightarrow G/N,f(a)=[a]_N$ ， $Kerf$ 为 $N$ ，因为商群的单位元是 $N$
$m$ 次方映射
$f:G\rightarrow G,f(a)=a^m$ ， $G$ 是阿贝尔群
雅可比映射
$J_n:Z_n^*\rightarrow \{\pm 1\},J_n(a)=(\frac{a}{n})$

同态的性质

$f(e)=e'$
$f(a^{-1})=f(a)^{-1}$ （互为逆元的元素的像仍互为逆元）
$H$ 是 $G$ 的子群 $\Leftrightarrow f(H)$ 是 $G'$ 的子群
$Imf$ 是 $G'$ 的子群， $Kerf$ 是 $G$ 的子群
群同态的复合还是群同态
$Kerf$ 是正规子群
$f(a)=f(b)\Leftrightarrow a\equiv b(mod\quad Kerf)$
$f$ 是单射当且仅当 $Kerf=\{e\}$ ， $f$ 是满射当且仅当 $Imf=G'$

基本同态定理（第一同构定理）

设 $f:G\rightarrow G'$ 是一个群 $G$ 到群 $G'$ 的同态，则存在唯一的 $G/ker(f)$ 到 $f(G)$ 的同构 $\rho$
$G/Kerf\cong Imf\\ \rho:[a]_{Kerf}\rightarrow f(a)$
并且 $f=i\circ\rho\circ s$

$s$ 是群 $G$ 到商群 $G/Kerf$ 的自然同态
$i$ 是 $f(G)$ 到 $G'$ 的恒等同态

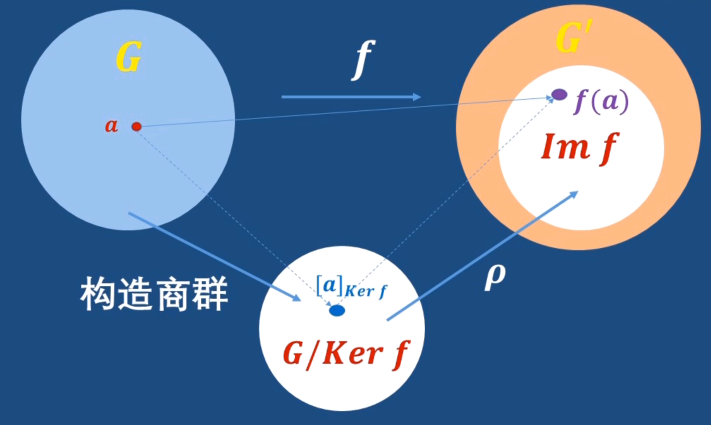
即：设 $s:G\rightarrow G/N$ 是一个同态映射，则对每一个 $a\in G$ ， $f(a)=\rho\circ s(a)$

第9章群的结构

元素的阶

设 $G$ 是群， $a\in G$ ，如果 $n$ 是满足
$a^n=e$
的最小正整数，则称 $n$ 是元素 $a$ 的阶，记为 $ord(a)$ ，不存在阶则为无限阶

元素阶的性质

$ord(a)=ord(a^{-1})$
若 $a^m=e$ ，则 $m|ord(a)$
$ord(a^m)=\frac{ord(a)}{(ord(a),m)}$
若 $ab=ba,\ gcd(ord(a),ord(b))=1$ ，则 $ord(ab)=ord(a)ord(b)$

循环群

设 $G$ 是群， $g\in G$ ，如果 $G=\langle g\rangle$ ，则称 $G$ 是循环群， $g$ 是循环群 $G$ 的生成元
如 $(Z,+)=\langle 1\rangle=\langle -1\rangle,(mZ,+)=\langle m\rangle=\langle -m\rangle,(Z_5,\times)=\langle 2\rangle=\langle 3\rangle$
根据群元素个数可分为无限循环群和有限循环群

循环群的性质

循环群都是阿贝尔群
循环群的子群是循环群
循环群的商群是循环群，生成元为 $\langle [g]_H\rangle$
若 $g^k=g^l$
对于无限循环群， $k=l$
对于有限循环群， $|G|{\large |} k-l$
$p$ 是素数， $Z_p^*$ 是 $p-1$ 阶循环群，若生成元为 $[g]$ ，则称 $g$ 是 $Z$ 的一个模 $p$ 原根
无限循环群的子群为 $\{\langle g^d\rangle|d=0,1,2\dots\}$ ， $n$ 阶循环群的全部子群为 $\{\langle g^d\rangle|d为n的因子\}$
无限循环群有且仅有两个生成元 $g,g^{-1}$ ， $n$ 阶有限循环群有 $\varphi (n)$ 个生成元，为 ${a^r|(n,r)=1}$
$G$ 是有限群，元素 $a$ 的阶是 $|G|$ 的因子，生成元的阶等于 $|G|$
素数阶的群必然是（有限）循环群。
$G$ 是 $n$ 阶有限循环群， $d$ 是 $n$ 的正因子， $G$ 里的 $d$ 阶元素一共有 $\varphi (d)$ 个

循环群的同构

无限循环群同构于 $Z$ ； $n$ 阶有限循环群同构于 $Z_n$

置换群与对称群

设 $S$ 是一个非空集合。 $G$ 是 $S$ 到自身的所有一一对应的映射 $f$ 组成的集合， $G=\{f|f是S上的变换\}$ ，则 $G$ 关于映射的复合运算构成的群称为 $S$ 上的对称群。
$S$ 是 $n$ 元有限集时, $G$ 叫做 $n$ 元对称群，记作 $S_n$ 。 $n$ 元对称群的任意一个子群，都叫做一个 $n$ 元置换群。
$G$ 中的元素叫做 $S$ 的一个置换。即置换是 $S$ 到自身的一个一一对应的映射。
$n$ 元置换全体组成的集合 $S_n$ 对置换乘法构成一个群，其阶为 $n!$

置换的乘法

$\sigma=\begin{pmatrix}1 & 2 & 3 & 4 & 5\\4 & 2 & 5 & 3 & 1\end{pmatrix},\tau=\begin{pmatrix}1 & 2 & 3 & 4 & 5\\3 & 5 & 4 & 2 & 1\end{pmatrix}$ ，计算 $\sigma\tau$
$\begin{align} \sigma\tau & =\begin{pmatrix}1 & 2 & 3 & 4 & 5\\4 & 2 & 5 & 3 & 1\end{pmatrix}\begin{pmatrix}1 & 2 & 3 & 4 & 5\\3 & 5 & 4 & 2 & 1\end{pmatrix}\\ & = \begin{pmatrix}3 & 5 & 4 & 1 & 2\\5 & 1 & 3 & 2 & 4\end{pmatrix}\begin{pmatrix}1 & 2 & 3 & 4 & 5\\3 & 5 & 4 & 2 & 1\end{pmatrix}\\ & = \begin{pmatrix}1 & 2 & 3 & 4 & 5\\5 & 1 & 3 & 2 & 4\end{pmatrix} \end{align}$

置换的轮换

对于不同 $n$ 个数，如果满足 $\sigma(i_k)=i_{k+1},\sigma(i_n)=i_0$
记作 $\sigma=\{i_1,i_2,\dots,i_k\}$ ，称为k-轮换
1-轮换称为恒等置换，2-轮换叫做对换
两个轮换若不存在相同元素，叫做不相交，不相交的轮换满足交换律

例： $\sigma=\begin{pmatrix}1 & 2 & 3 & 4 & 5\\4 & 2 & 5 & 3 & 1\end{pmatrix}$ ，计算将其表示为轮换
$\begin{align} & \sigma(1)=4,\sigma(4)=3,\sigma(3)=4,\sigma(5)=1\\ & \sigma(2)=2\\ & \sigma=(1,4,3,5)(2) \end{align}$
任意置换都可以表示为一些不相交的轮换的乘积，在不考虑次序的情况下，该表达式是唯一的

例：
$\begin{pmatrix}1 & 2 & 3 & 4 & 5 & 6 & 7 & 8\\3 & 8 & 6 & 7 & 4 & 1 & 5 & 2\end{pmatrix}\\ \begin{align} & 1\rightarrow 3\rightarrow 6\rightarrow 1\\ & 2\rightarrow 8\rightarrow 2\\ & 4\rightarrow 7\rightarrow 5\rightarrow 4\\ & \sigma=(1,3,6)(2,8)(4,7,5) \end{align}$
k-轮换可以表示为2-轮换的乘积
$(a_1,a_2,\dots,a_n)=(a_1,a_n)(a_1,a_{n-1})\dots (a_1,a_2)$

$\begin{pmatrix}1 & 2 & 3\\2 & 3 & 1\end{pmatrix}=\begin{pmatrix}1 & 2 & 3\\3 & 2 & 1\end{pmatrix}\begin{pmatrix}1 & 2 & 3\\2 & 1 & 3\end{pmatrix}=(1,3)(1,2)\ne (1,2)(1,3)\ 相交不满足交换律$

置换群

$n$ 元置换构成的群叫做 $n$ 元置换群

例：设 $\sigma_1=(1,2,3,4)\sigma_2=(1,3,2,4)$ ，则循环群
$G_{1}=\langle\sigma_{1}\rangle=\{e,(1,2,3,4),(1,3)(2,4),(1,4,3,2)\}\\ G_{2}=\langle\sigma_{2}\rangle=\{e,(1,3,2,4),(1,2)(3,4),(1,4,2,3)\}\\$
都是4元置换群.

第10章环与理想

环的定义

$R$ 对加法构成交换群，对乘法满足结合律和分配律，则 $R$ 叫做环

若 $R$ 对乘法还满足交换律，则 $R$ 叫做交换环
若 $R$ 对乘法有单位元，则 $R$ 叫做有单位元的环。零元与单位元可能一样也可能不一样
若存在非零元 $b(c)$ 使得非零元 $a$ 满足 $ab=0_R(ca=0_R)$ ，则 $a$ 称为左(右)零因子；如果它同时为左右零因子，则称 $a$ 为零因子， $R$ 叫做有零因子环
若存在非零元 $b(c)$ 使得非零元 $a$ 满足 $ab=1_R(ca=1_R)$ ，则 $b(c)$ 称为 $a$ 的右(左)逆；如果 $a$ 同时为左右逆元，则称 $a$ 为逆元
有单位元没零因子的交换环称为整环

环与域

若交换环 $K$ 满足 $K$ 对加法构成交换群， $K\backslash\{0\}$ 对乘法构成交换群，加法和乘法单位元不同，则称 $K$ 为域

交换环上的整除

因子(整除)：对于非零元 $a,b$ 如果 $c$ 使得 $a=cb$ ，就称 $b$ 整除 $a$ 或者 $a$ 被 $b$ 整除，记作 $b|a$ ， $b$ 叫做 $a$ 的因子， $a$ 叫做 $b$ 的倍元
真因子：如果 $b,c$ 不是单位元，则 $b$ 是 $a$ 的真因子
相伴元：若 $a|b$ 且 $b|a$ ，则称 $a$ 与 $b$ 相伴，记作 $a\sim b$ ，相伴关系是 $R$ 上的一个等价关系。 $a\sim b$ 等价于 $R$ 中存在可逆元 $u$ ，使得 $a=bu$ 。
不可约元(素元)：不是单位元且没有真因子
整数环中不可约元就是素数，多项式环中不可约元就是不可约多项式

环同态与同构

对于两个环 $R,R'$ ，如果映射 $f:R\rightarrow R'$ 满足以下条件

任意 $a,b\in R$ ，有 $f(a+b)=f(a)+f(b)$
任意 $a,b\in R$ ，有 $f(ab)=f(a)f(b)$

如果 $f$ 是一对一的，则为单同态；如果 $f$ 是满的，则为满同态；如果 $f$ 是一一对应的，则为同构

特征与素域

如果存在最小正整数 $P$ 使得任意 $a\in R$ ，都有 $pa=a+\dots+a=0$ ，则称环的特征为 $p$ ，若不存在这样的整数，则特征为0
如果域 $K$ 的特征不为0，则其特征必为素数
设 $R$ 是有单位元的交换环，如果特征为 $p$ ，则有 $(a+b)^p=a^p+b^p\quad a,b\in R$
设 $p$ 是素数， $f(x)=a_nx^n+\dots+a_1x+a_0$ 是整系数多项式，则 $[f(x)]^p=f(x^p)\ (mod\ p)$
不含真子域的域叫做素域
设 $F$ 是一个域。如果 $F$ 的特征为0，则 $F$ 有一个与 $Q$ 同构的素域。如果 $F$ 的特征为 $p$ ，则 $F$ 有一个与 $F_p$ 同构的素域

理想和商环

相当于群的陪集和商群

第11章多项式环

定义

设 $R$ 是整环， $x$ 为变量，则 $R$ 上形为
$f(x)=a_nx^n+\dots+a_1x+a_0\quad a_i\in R$
的元素称为 $R$ 上的多项式，多项式的次数 $deg\ f=n$
设 $R[x]$ 是整环R上的多项式符合上式，则对于多项式加法和乘法， $R[x]$ 是一个整环

多项式整除与不可约多项式

设f(x),g(x)是整环R上的多项式，其中g(x)\ne 0。如果存在一个多项式q(x)使得
f(x)=q(x)g(x)
则称g(x)整除f(x)或者f(x)被g(x)整除，记作g(x)\mid f(x)；若不整除，记作g(x)\nmid f(x)
- $g(x)|f(x),h(x)|g(x)\Rightarrow h(x)|f(x)\quad g(x),h(x)\ne 0$
- $h(x)|f(x),h(x)|g(x)\Rightarrow h(x)|s(x)f(x)+t(x)g(x)\quad f(x),g(x),h(x)\ne 0$
设 $f(x)$ 是域 $K$ 上的 $n$ 次可约多项式， $p(x)$ 是 $f(x)$ 的次数最小的非常数因式，则 $p(x)$ 一定是不可约多项式，且 $deg\ p\le \frac{1}{2}deg\ f$
设 $f(x)$ 是域 $K$ 上的多项式。如果对所有的不可约多项式 $p(x)$ ， $deg\ p\le \frac{1}{2}deg\ f$ ，都有 $p(x)\nmid f(x)$ ，则 $f(x)$ 一定是不可约多项式。

多项式欧几里德除法

$f(x)=q(x)g(x)+r(x),deg\ r\lt deg\ g$
$q(x)$ 叫不完全商， $r(x)$ 叫余式
$f(x)=q(x)(x-a)+f(a)$
对于次数不大于3的多项式， $x-a|f(x)$ 的充要条件是 $f(a)=0$
多项式有类似整数和环的以下概念

最大公因式 $(f(x), g(x))$
$f(x)=q(x)g(x)+h(x)\Rightarrow (f(x),g(x))=(g(x),h(x))$
$(f(x), g(x))=r_k(x)\quad deg\ g\ge 1$ ， $r_k(x)是最后一个非零余式$
$s(x)f(x)+t(x)g(x)=(f(x), g(x))$
同余 $f(x)≡ g(x)(mod\ m(x))$
记 $[r(x)]=r(x)(mod\ m(x))$ 为 $f(x)$ 所在的同余等价类， $r(x)$ 为最小余式
设p(x)是K[x]中的多项式，则(p(x))=\{f(x)|f(x)∈K[x], p(x)|f(x)\}是K[x]中的理想。由此得到商环K[x]/(p(x))。该商环上的运算法则为
- 加法： $f(x)+g(x) = ((f+g)(x) (mod\ p(x)))$
- 乘法： $f(x) · g(x) = ((f·g)(x) (mod\ p(x)))$
商环 $K[x]/(p(x))$ 对于加法和乘法构成一个域

本原多项式

设 $p$ 是素数， $p(x)$ 是 $F_p[x]$ 中的 $n$ 次不可约多项式，则
$F_[x]/(p(x))=\{a_{n-1}x^{n-1}+\dots+a_1x+a_0|a_i\in F_p\}$
记作 $F_{p^n}$ 。这个域的元素个数为 $p^n$

例：设 $p(x)=x^8+x^4+x^3+x+1$ 是 $F_2[x]$ 中的8次不可约多项式，有
$F_{2^8}=F_2[x]/(p(x))=\{a_7x^7+\dots+a_1x+a_0|a_i\in\{0,1\}\}$
设 $p$ 是素数， $f(x)$ 是 $F_p[x]$ 中的n次多项式，则使得
$x^e\equiv 1 (mod\ f(x))$
成立的最小正整数 $e$ 叫做 $f(x)$ 在 $F_p$ 上的指数，记作 $ord_p(f(x))$
如果 $ord_p(f(x))=p^n-1$ ，则称 $f(x)$ 为 $F_p$ 上的本原多项式.

例： $f(x)=x^2-2\in F_5[x]$ 是否为本原多项式
$\begin{align} & p=5,n-2,验证是否ord_p(f(x))=5^2-1=24\\ & f(x)=x^2-2可得有一解\alpha,\alpha^2=2,令a_1=\alpha\\ & a_1^0=1,a_1^1=\alpha,a_1^2=2,\dots,a_1^7=3\alpha,a_1^8=1\\ & ord_p(f(x))=8\ne 25,不是本元多项式\\ \end{align}$
本元多项式是不可约多项式
设 $p$ 是素数， $n$ 是正整数， $f(x)$ 是 $F_p[x]$ 中的 $n$ 次多项式。如果
$\begin{align} & x^{p^n-1}\equiv 1(mod\ f(x))\\ & x^{\frac{p^n-1}{q_i}}\not\equiv 1(mod\ f(x))\quad q_i是p^n-1的不同素因数 \end{align}$
则 $f(x)$ 是 $n$ 次本元多项式

例：证明 $f(x)= x^4+x+1$ 是 $F_2[x]$ 的本元多项式
$\begin{align} & p=2,n=4,p^2-1=15,q_1=3,q_2=5,\frac{p^n-1}{q_1}=5,\frac{p^n-1}{q_2}=3\\ & 要验证x^{15}是否和1同余，x^3,x^5是否都不同余于1\\ & x^{15}\equiv 1(mod\ f(x))\\ & x^5\not\equiv 1(mod\ f(x)),x^3\not\equiv 1(mod\ f(x)) \end{align}$
所以是本元多项式

第12章域和Galois理论

域的扩张

设 $F$ 为一个域，如果 $K$ 是 $F$ 的子域，则称 $F$ 为 $K$ 的扩域
特征为0的域是 $Q$ 的扩域，特征为 $p$ 的域是 $F_p$ 的扩域

实数域 $R$ 为有理数域 $Q$ 的扩域
$F_{2^8}=F2[x]/(x8+x4+x3+x+1)是F_2$ 的扩域；
$F$ 为域 $K$ 的一个扩张，将 $F$ 看成 $K$ 上的向量空间，若是有限维的，则称 $F$ 为 $K$ 的有限维扩张， $K$ 上向量空间 $F$ 的维数称为扩张次数，记为 $[F:K]$

第1章 整数的可除性