计量经济学

一元线性回归模型

简单回归模型

OLS

用样本的\hat\beta_0,\hat\beta_1估计\beta_0,\beta_1
目标:\min_{\hat\beta_0,\hat\beta_1} \sum_{i = 1}^n[y_i-\hat\beta_0-\hat\beta_1x_i]^2
\therefore \begin{cases} \frac{\partial\sum_{i = 1}^{n}(y_i-\hat\beta_0-\hat\beta_1x_i)^2}{\partial\hat\beta_0}=0 \\ \frac{\partial\sum_{i = 1}^{n}(y_i-\hat\beta_0-\hat\beta_1x_i)^2}{\partial\hat\beta_1}=0 \end{cases} \Rightarrow \begin{cases} \sum_{i = 1}^{n}(y_i-\hat\beta_0-\hat\beta_1x_i)=0 & \text{ \textcircled{1} } \\ \sum_{i = 1}^{n}x_i(y_i-\hat\beta_0-\hat\beta_1x_i)=0 & \text{ \textcircled{2} } \end{cases}
由\textcircled{1}得
\bar y=\hat\beta_0+\hat\beta_1\bar x
\textcircled{1}带入\textcircled{2}得
\sum_{i = 1}^{n}x_i[y_i-(\bar y-\hat\beta_1\bar x)-\hat\beta_1x_i]=0
所以
\sum_{i = 1}^{n}x_i(y_i-\bar y)=\hat\beta_1\sum_{i = 1}^{n}x_i(x_i-\bar x)
将x_i换为x_i-\bar x可得
\begin{align} \sum_{i = 1}^{n}(x_i-\bar x)(y_i-\bar y)&=\hat\beta_1\sum_{i = 1}^{n}(x_i-\bar x)(x_i-2\bar x)\\ &=\hat\beta_1\sum_{i = 1}^{n}[(x_i-\bar x)^2-\bar x(x_i-\bar x)]\\ &=\hat\beta_1\sum_{i = 1}^{n}(x_i-\bar x)^2-\hat\beta_1\bar x\sum_{i = 1}^{n}(x_i-\bar x)\\ &=\hat\beta_1\sum_{i = 1}^{n}(x_i-\bar x)^2 \end{align}\\ \therefore\hat\beta_1=\frac{\sum_{i = 1}^{n}(x_i-\bar x)(y_i-\bar y)}{\sum_{i = 1}^{n}(x_i-\bar x)^2}=\frac{s_{xy}}{s_x^2}
若已知\beta_0为0
则\textcircled{2}化为
\sum_{i = 1}^{n}x_i(y_i-\hat\beta_1x_i)=0\\ \therefore\hat\beta_1=\frac{\sum_{i = 1}^{n}x_iy_i}{\sum_{i = 1}^{n}x_i^2}

拟合值与残差

OLS拟合值与残差分别为
\begin{align} &\hat y_i=\hat\beta_0+\hat\beta_1x_i\\ &\hat u_i=y_i-\hat y_i \end{align}
由\textcircled{1}可知
\begin{align} &\sum_{i=1}^{n}\hat u_i=0\\ &\bar{\hat u}=\frac{\sum_{i=1}^{n}\hat u_i}{n}=0\\ &\bar y=\beta_0+\beta_1\bar x \end{align}
但对于没有常数项的回归，式\textcircled{1}不存在，
由\textcircled{2}可知
\sum_{i=1}^{n}x_i{\hat u_i}=0\\ \begin{align} &\therefore\sum_{i=1}^{n}(x_i-\bar x)(\hat u_i-\bar{\hat u})\\ &=\sum_{i=1}^{n}(x_i\hat u_i-\bar x\hat u_i)-\bar{\hat u}\sum_{i=1}^{n}(x_i-\bar x)\\ &=\sum_{i=1}^{n}x_i\hat u_i-\bar x\sum_{i=1}^{n}\hat u_i\\ &=0\end{align}

期望

假设：

1. 模型关于参数线性
2. 随机抽样
3. x_i不是完全相同的数值
4. E(u|x)=0
   \begin{align} \hat\beta_1 &=\frac{\sum_{i = 1}^{n}(x_i-\bar x)(y_i-\bar y)}{\sum_{i = 1}^{n}(x_i-\bar x)^2}\\ &=\frac{\sum_{i = 1}^{n}(x_i-\bar x)y_i}{s_x^2}\\ \end{align}\\ \begin{align} &\sum_{i = 1}^{n}(x_i-\bar x)y_i\\ &=\sum_{i = 1}^{n}(x_i-\bar x)(\beta_0+\beta_1x_i+u_i)\\ &=\beta_0\sum_{i = 1}^{n}(x_i-\bar x)+\beta_1\sum_{i = 1}^{n}x_i(x_i-\bar x)+\sum_{i = 1}^{n}u_i(x_i-\bar x)\\ &=0+\beta_1\sum_{i = 1}^{n}(x_i-\bar x)^2+\sum_{i = 1}^{n}u_i(x_i-\bar x)\\ &=\beta_1s_x^2+\sum_{i = 1}^{n}u_i(x_i-\bar x) \end{align}\\ \therefore \hat{\beta_1}=\beta_1+\frac{\sum_{i = 1}^{n}u_i(x_i-\bar x)}{s_x^2}
   所以\beta_1是关于u_i的随机变量，u_i取决于样本的选取
   \begin{align} E(\hat{\beta_1}) &=\beta_1+\frac{\sum_{i = 1}^{n}\bar u_i(x_i-\bar x)}{s_x^2}\\ &=\beta_1 \end{align}
   当E(u_i)=0,\hat{\beta_1}无偏
   \begin{align} E(\hat{\beta_0}) &=E(\bar y-\hat{\beta_1}\bar x)\\ &=E(\beta_0+\beta_1\bar x+\bar u-\hat{\beta_1}\bar x)\\ &=\beta_0+\beta_1\bar x+0-\beta_1\bar x\\ &=\beta_0 \end{align}
   进而\hat{\beta_0}无偏

方差

额外假设：同方差Var(u|x)=\sigma^2
\begin{align} Var(\hat{\beta_1}) &=Var(\beta_1+\frac{\sum u_i(x_i-\bar x)}{s_x^2})\\ &=\frac{\sum Var(u_i)(x_i-\bar x)^2}{s_x^4}\\ &=\frac{\sigma^2\sum (x_i-\bar x)^2}{s_x^4}\\ &=\frac{\sigma^2}{s_x^2} \end{align}\\ \begin{align} Var(\hat{\beta_0}) &=Var(\bar y-\hat{\beta_1}\bar x)\\ &=Var(\beta_0+\beta_1\bar x+\bar u-\hat{\beta_1}\bar x)\\ &=\frac{\sigma^2\bar{x^2}}{s_x^2} \end{align}
观测值变差越大、误差项方差越小、样本容量越大越精确
若不满足同方差则
Var(\hat{\beta_1})=\frac{\sum \sigma_i^2(x_i-\bar x)^2}{s_x^4}
\sigma^2无法直接获取，需要利用残差估计
\begin{align} \because \hat u_i &=y_i-\hat y_i\\ &=\beta_0+\beta_1x_i+u_i-\hat{\beta_0}-\hat{\beta_1}x_i\\ &=u_i-(\hat{\beta_0}-\beta_0)-(\hat{\beta_1}-\beta_1)x_i\\ \therefore 0 &=\bar{\hat u_i}\\ &=\bar u-(\hat{\beta_0}-\beta_0)-(\hat{\beta_1}-\beta_1)x_i \end{align}
两式做差得
\hat u_i=(u_i-\bar u)-(\hat{\beta_1}-\beta_1)(x_i-\bar x)
两边平方后求和再取期望
E[\sum{\hat u_i}^2]=E[\sum(u_i-\bar u)^2]+E[\sum(\hat{\beta_1}-\beta_1)^2(x_i-\bar x)^2]-2E[\sum(u_i-\bar u)(\hat{\beta_1}-\beta_1)(x_i-\bar x)]
其中
\begin{align} & \begin{align} E[\sum(u_i-\bar u)^2] &=\sum E(u_i^2)-2E(\bar u\sum u_i)+nE{\bar u}^2\\ &=n\sigma^2-2\sigma^2+\sigma^2\\ &=(n-1)\sigma^2\\ \end{align}\\ & \begin{align} E[\sum(\hat{\beta_1}-\beta_1)^2(x_i-\bar x)^2] &=Var(\hat{\beta_1})\sum(x_i-\bar x)^2\\ &=\sigma^2\\ \end{align}\\ & \begin{align} E[\sum(u_i-\bar u)(\hat{\beta_1}-\beta_1)(x_i-\bar x)] &=\frac{E[\sum(u_i-\bar u)(x_i-\bar x)\sum u_i(x_i-\bar x)]}{s_x^2}\\ &=\sigma^2 \end{align}\\ \therefore\quad & E[\sum{\hat u_i}^2]=(n-2)\sigma^2\\ & \hat{\sigma^2}=\frac{\sum{\hat u_i}^2}{n-2}\\ & \hat{Var(\hat\beta)}=\frac{\hat{\sigma^2}}{s_x^2} \end{align}

经典线性模型

前五条假设被称为高斯-马尔可夫假设，在该假定下，OLS估计量是最优线性无偏估计量（BLUE）
若u服从均值为0方差为\sigma^2的正态分布则满足正态性假定
高斯-马尔可夫假定+正态性假定被称为经典线性模型假定（CLM）
在大样本情况下可以放弃正态性假定
在CLM假定下，对于给定样本
\hat\beta_j\sim Normal[\beta_j,Var(\hat\beta_j)]

大样本性质

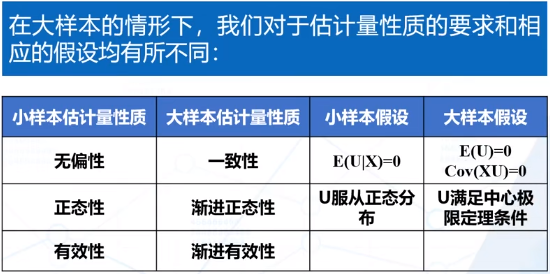
一致性（相合性）：n趋向无穷时，估计量的分布紧缩成一个参数值。需要前四条假设
\begin{align} Plim\hat{\beta_1} &=Plim(\beta_1+\frac{n^{-1}\sum u_i(x_i-\bar x)}{n^{-1}s_x^2})\\ &=\beta_1+\frac{Cov(X,u)}{Var(X)}\\ &=\beta_1 \end{align}
利用到Cov(X,u)=0和E(u)=0，弱于假定E(u|X)=0
若不满足假设，则有偏且不一致
渐进正态性：若数据满足中心极限定理，即使u不满足正态性，估计量也具有正态性
\hat{\beta_1}=\beta_1+\frac{n^{-1}\sum u_i(x_i-\bar x)}{n^{-1}s_x^2}
分母依概率收敛到有限的数，分子依分布收敛到正态分布，因此分式满足依分布收敛，利用中心极限定理满足正态性
\begin{align} & \hat\beta_1\sim Normal[\beta_1,\frac{Var[(X_i-\mu_x)u_i]}{n[Var(X_i)]^2}]\\ & \hat\beta_0\sim Normal[\beta_0,\frac{Var(H_iu_i)}{n[E(H_i^2)^2]}],H_i=1-\frac{\mu_XX_i}{E(X_i^2)} \end{align}
标准误以\frac{1}{\sqrt n}收敛至0；在同方差情况下公式可以简化
渐进有效性：随着样本越大，OLS估计量可以达到理论上的最小方差

方差分析

R^2=\frac{ESS}{TSS}=\frac{\sum (\hat Y_i-\bar Y)^2}{\sum (Y_i-\bar Y)^2}
残差和为0时，0\leq R^2 \leq 1

零条件期望假设与矩估计

E(u|x)=0
可得
E(y|x)=\beta_0+\beta_1x
从E(u|x)=0，我们有两个关于母体期望的假设
\begin{align} &E(u)=0\\ &Cov(x,u)=E(xu)=0\\ \therefore &n^{-1}\sum_{i = 1}^{n}(y_i-\hat\beta_0-\hat\beta_1x_i)=0\\ &n^{-1}\sum_{i = 1}^{n}x_i(y_i-\hat\beta_0-\hat\beta_1x_i)=0 \end{align}
矩估计与OLS求导结果相同，说明OLS估计量能很好的近似母体性质

多元线性回归模型

遗漏变量偏误

\begin{align} Plim (\hat{\beta_1}-\beta_1) &=Plim \frac{\frac{1}{n-1}\sum (x_i-\bar x)u_i}{\frac{1}{n-1}\sum (x_i-\bar x)^2}\\ &=\frac{\sigma_{xu}}{\sigma_x^2}\\ &=\frac{\sigma_u}{\sigma_x}\times\frac{\sigma_{xu}}{\sigma_x\sigma_u}\\ &=\rho_{xu}\times\frac{\sigma_u}{\sigma_x} \end{align}
若\rho_{xu}\neq 0则\hat{\beta_1}有偏且不一致，就叫做遗漏变量偏误
遗漏变量要满足两个条件：z是y的决定因素（即z是u的一部分）；z与x相关（即corr(z,x)\neq 0）

总体多元回归模型

OLS

目标:\min_{\hat\beta_0,\hat\beta_1,\dots,\hat\beta_k} \sum_{i = 1}^n[y_i-\hat\beta_0-\hat\beta_1x_{i1}-\dots-\hat\beta_kx_{ik}]^2
(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y}=(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{X}\mathbf{\hat{\beta}}+(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{\hat u}=\mathbf{\hat{\beta}}+0=\mathbf{\hat{\beta}}

偏效应

考虑y_i=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+u_i
则
\hat y=\hat{\beta_0}+\hat{\beta_1}x_1+\hat{\beta_2}x_2\\ \hat{\beta_1}=\frac{\sum \hat{r_{i1}}y_i}{\sum {\hat{r_{i1}}}^2}\\ \text{其中}\hat{x_{i1}}=\hat{\delta_0}+\hat{\delta_1}\hat x_{i2},\hat r_{i1}=x_{i1}-\hat x_{i1}
这意味着x_1中与x_2无关的部分与y相关，我们估计的系数是排除了x_2的影响后x_1和y的样本关系
若\widetilde y=\widetilde\beta_0+\widetilde\beta_1x_1,x_2对x_1做简单线性回归的斜率系数为\hat{\delta_1}
则有
\widetilde\beta_1=\hat{\beta_1}+\hat{\beta_2}\hat{\delta_1}
只有当\hat{\beta_2}=0或x_1,x_2不相关时才有\widetilde\beta_1=\hat{\beta_1}

调整R2

{\bar R}^2=1-\frac{n-1}{n-k-1}(1-R^2)\lt R^2
若回归方程没有常数项，SST不再等于SSE+SSR，OLS残差样本均值不为0，{\bar R}^2可能为负

假设条件

1. 总体模型线性
2. 随机抽样
3. 不存在完全共线性
4. E(u|x_1,x_2,\dots,x_k)=0

不完全共线性

导致至少一个回归变量的方差变大，不影响无偏性和一致性

期望

1. 在四条假设下
   E(\hat\beta_j)=\beta_j,j=0,1,\dots,k
   如果模型中包含了本不应该包含的变量，不会影响系数估计和OLS的无偏性，但是包含无关变量对OLS估计量的方差具有不利影响
   如果我们遗漏了一个应该包含在模型中的变量，OLS估计量是有偏的

2. 假如真实模型为y=\beta_0+\beta_1x_1+\beta_2x_2+u
   估计模型为\widetilde y=\widetilde\beta_0+\widetilde\beta_1x_1+v
   则
   \widetilde\beta_1=\beta_1+\beta_2\frac{\sum (x_{i1}-\bar{x_1})x_{i2}}{\sum (x_{i1}-\bar{x_1})}+\frac{\sum (x_{i1}-\bar{x_1})u_i}{\sum (x_{i1}-\bar{x_1})}\\ \frac{\sum (x_{i1}-\bar{x_1})x_{i2}}{\sum (x_{i1}-\bar{x_1})}是x_2对x_1回归的系数

方差

1. 同方差假定
   Var(u|\mathbf X)=\sigma^2
   五条假定合称横截面回归的高斯-马尔可夫假定
   在高斯-马尔可夫假定下
   Var(\hat{\beta_j})=\frac{\sigma^2}{SST_j(1-R_j^2)}\\ SST_j=\sum_{i=1}{n}(x_{ij}-\bar x_j)^2
   R_j^2是将x_j对其它自变量回归得到的R^2，SSR_J\j是该回归的残差平方和
   误差项方差越大、样本总变异越小、参数间线性关系越强，OLS估计量方差越大
   Var(\hat{\beta_j})=\frac{\sigma^2}{SST_j(1-R_j^2)}=VIF_j\times\frac{\sigma^2}{SST_j}
   若方差膨胀因子大于10，共线性越高，方差越大

2. 假如真实模型为y=\beta_0+\beta_1x_1+\beta_2x_2+u
   估计模型为\widetilde y=\widetilde\beta_0+\widetilde\beta_1x_1+v
   则
   Var(\widetilde\beta_1)=\frac{\sigma^2}{SST_1}\le Var(\hat\beta_1)=\frac{\sigma^2}{SST_1(1-R_1^2)}

   • 当\beta_2\ne 0，\widetilde\beta_1有偏，\hat\beta_1无偏，且有Var(\widetilde\beta_1)\lt Var(\hat\beta_1)
   • 当\beta_2=0，\widetilde\beta_1,\hat\beta_1均无偏，且有Var(\widetilde\beta_1)\lt Var(\hat\beta_1)
   • 只有在x_1，和x_2，不相关时，两个估计量的方差才相等

3. 利用残差估计\sigma^2
   \hat\sigma^2=\frac{\sum \hat u_i^2}{n-k-1}\equiv\frac{SSR}{df}
   在五条假定下，估计量无偏

经典线性模型

前五条假设被称为高斯-马尔可夫假设，在该假定下，OLS估计量是最优线性无偏估计量（BLUE）
若定u独立于\mathbf X，服从均值为0方差为\sigma^2的正态分布则满足正态性假定
高斯-马尔可夫假定+正态性假定被称为经典线性模型假定（CLM）
在CLM假定下，对于给定样本
\hat\beta_j\sim Normal[\beta_j,Var(\hat\beta_j)]

单个系数的假设检验

1. \hat\beta_j\sim Normal[\beta_j,\frac{\sigma^2}{SST_j(1-R_j^2)}]
   但是\sigma^2未知，使用估计值替代

2. 在CLM假设条件下
   \begin{align} & \frac{\hat\beta_j-\beta_j}{se(\hat\beta_j)}\sim t(n-k-1)\\ & se(\hat\beta_j)=\frac{\hat\sigma}{\sqrt{SST_j(1-R_j^2)}} \end{align}

3. t检验
   如
   H_0:\beta_j=\beta\quad vs.\quad H_1:\beta_j\ne\beta
   构造t统计量
   t_{\hat\beta_j}=\frac{\hat\beta_j-\beta}{se(\hat\beta_j)}\sim t(n-k-1)
   查表确定\frac{\alpha}{2}对应的值C，若|t_{\hat\beta_j}|\gt C则拒绝

单个系数的置信区间及系数组合的检验

1. 置信区间
   [\hat\beta_j -t_{n-k-1}(\frac{\alpha}{2})\times se(\hat\beta_j),\hat\beta_j +t_{n-k-1}(\frac{\alpha}{2})\times se(\hat\beta_j)]

2. 参数线性组合的假设检验
   如
   H_0:\beta_1=\beta_2\quad vs.\quad H_1:\beta_1\ne\beta_2
   构造t统计量
   \begin{align} & t=\frac{\hat\beta_1-\hat\beta_2}{se(\hat\beta_1-\hat\beta_2)}\sim t(n-k-1)\\ & se(\hat\beta_1-\hat\beta_2)=\sqrt{Var(\hat\beta_1)+Var(\hat\beta_2)-2Cov(\hat\beta_1,\hat\beta_2)} \end{align}

3. 重写模型
   如
   y=\beta_0+\beta_1x_1+\beta_2x_2\Leftrightarrow y=\beta_0+(\beta_1-\beta_2)x_1+\beta_2(x_2+x_1)

多个线性组合的约束和F检验

1. 若y=\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_kx_k+u
   H_0:\beta_{k-q+1}=0,\dots,\beta_k=0\quad vs.\quad H_1:\beta_{k-q+1},\dots,\beta_k不全为0
   考虑两个模型
   \begin{align} & H_0成立:r\rightarrow y=\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_{k-q}x_{k-q}+u\\ & H_1成立:ur\rightarrow y=\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_qx_k+u\\ \end{align}
   比较两个模型的残差平方和差别大不大
   \begin{align} F & \equiv\frac{(SSR_r-SSR_{ur})/q}{SSR_{ur}/(n-k-1)}\\ & \equiv\frac{(R_{ur}^2-R_{r}^2)/q}{1-R_{ur}^2/(n-k-1)}\quad\quad (SSR=SST(1-R^2))\\ 若 & k=q则R_{r}^2=0\\ F & \equiv\frac{R^2/k}{1-R^2/(n-k-1)} \end{align}

   • F\gt 0因为受约束模型的SSR大于不受约束模型
   • F值度量的是SSR从不受约束模型到受约束模型的相对增加量
   • q=约束条件的个数，n-k-1= df_{ur}
   • 只适用于同方差
   • 如果只检验一个约束条件，此时F=t^2，p值相同

2. 在CLM假设下
   F\sim F(q,n-k-1)

3. 一般线性约束
   如y=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3+u\quad H_0:\beta_1=1,\beta_3=0
   代入约束条件：y=\beta_0+x_1+\beta_2x_2+u
   与原式比较计算

多元回归模型OLS估计的渐进性

1. 证明
   \begin{align} Plim\mathbf{\hat\beta} & =\mathbf\beta+Plim((\mathbf{X'}\mathbf{X})^{-1}\mathbf{X'}u)\\ & =\mathbf\beta+Plim(n^{-1}\mathbf{X'}\mathbf{X})^{-1}Plim(n^{-1}\mathbf{X'}u)\\ & =\mathbf\beta+\mathbf c\times 0\\ & =\mathbf\beta \end{align}
   可以放款零均值假设，只需要
   \begin{align} & E(u)=0\\ & Cov(x_j,u)=0,j=1,2,\dots,k \end{align}

2. OLS估计的渐近正态和大样本推断

   • 在CLM假设下，\hat\beta的抽样分布是正态的，因此可以推导出常用的t分布和F分别
   • OLS估计量的正态性，关键取决于总体中误差分布的正态性
   • 正态性假定意味着给定x时，y的分布也是正态的
   • 如果正态性不满足，不会影响OLS在高斯马尔可夫假定下成为最优线性无偏估计的结论，会影响估计量的方差的无偏性
   • 基于中心极限定理，任何形态的总体都满足渐进正态性，可以放宽对u正态性的要求

3. 渐进标准误
   当n很大

   • 近似有
     \begin{align} & \sqrt{n}(\hat\beta_j-\beta_j)\sim N(0,\frac{\sigma^2}{a_j^2})\\ & a_j^2=Plim(\frac{\sum_i \hat{r}_{ij}^2}{n}) \end{align}
     \hat r_{ij}是x_j关于其它所有自变量进行回归的残差
   • \hat{\sigma}^2=\frac{SSR}{n-k-1}是\sigma^2的一致估计量从而得到se(\hat\beta_j)
   • 近似有
     \frac{\hat\beta_j-\beta_j}{se(\hat\beta_j)}\sim N(0,1)
   • se(\hat\beta_j)\approx\frac{1}{\sqrt n}\times\frac{\hat\sigma_j}{a_j}，以\frac{1}{\sqrt n}速度收敛
   • 需要满足同方差

异方差条件下的假设检验

1. 为什么要担心异方差性？

   • 即使我们不假设同方差性，OLS仍是无偏且一致的，但是如果是异方差的，估计的标准误是有偏的
   • 如果标准误有偏，我们就不能使用通常的t统计量或F统计量进行推断

2. 异方差稳健标准误
   Var(\hat\beta_j)=\frac{\sum_{i=1}^{n}\hat r_{ij}\hat u_i^2}{SSR_j^2}
   有时方差乘以\frac{n}{n-k-1}来矫正自由度

3. 异方差条件下的t统计量
   \begin{align} & t=\frac{\hat\beta_j-\beta}{se(\hat\beta_j)}\sim N(0,1)\\ & se(\hat\beta_j)=\sqrt{\frac{\sum_{i=1}^{n}\hat r_{ij}^2\hat u_i^2}{SSR_j^2}} \end{align}
   需要大样本

4. 有q个约束条件的联合假设检验
   异方差稳健统计量F
   F\sim F(q,\infty)=\frac{\chi (q)}{q}

非线性回归模型

多项式回归

1. 形式
   y_{i}=\beta_{0}+\beta_{1} x_{i}+\beta_{2} x_{i}^{2}+\cdots+\beta_{r} x_{i}^{r}+u_{i}
2. 含有二项式的模型
   形如y=\beta_{0}+\beta_{1} x+\beta_{2} x^{2}+u
   \begin{align} & \Delta \hat{y} \approx\left(\widehat{\beta}_{1}+2 \widehat{\beta}_{2} x\right) \Delta x \\ & \frac{\Delta \hat{y}}{\Delta x} \approx \widehat{\beta}_{1}+2 \widehat{\beta}_{2} x \end{align}

对数回归

对数变换将变量的变化转化为百分率的形式（比如弹性），而不是线性的形式。

1. 形式
   \begin{align} 线性对数模型 & \quad y=\beta_0+\beta_1 ln(x)+u\\ 对数线性模型 & \quad ln(y)=\beta_0+\beta_1 x+u\\ 双对数模型 & \quad ln(y)=\beta_0+\beta_1 ln(x)+u\\ \end{align}
   以双对数模型为例，\frac{\Delta y}{y}=\beta_1\frac{\Delta x}{x}，即为弹性
   • 哪种变量经常取对数形式？
     以正的美元数量为单位的变量
     人口等大正整数变量
   • 哪种变量通常以原有形式出现？
     以年度量的变量
     比例或百分比变量

含有交互项的模型

1. 两个二值变量的交互作用
   y=\beta_0+\beta_1D_1+\beta_2D_2+\beta_3(D_1\times D_2)+u
   \beta_3表示某一项为1时，另一项效应的增量

2. 两个连续变量的交互作用
   y=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3(x_1\times x_2)+u
   此时
   \frac{\partial y}{\partial x_1}=\beta_1+\beta_3x_2
   \beta_3表示某一项增加时，另一项效应的增量

虚拟变量

虚拟变量是值为0或1的变量，又叫二元变量或哑变量

含有一个虚拟自变量的回归

定义一个虚拟变量female
wage=\beta_0+\beta_1edu+\delta_0female
\delta_0就是男女平均工资之差

虚拟变量陷阱

虚拟变量和常数项完全共线性

涉及虚拟变量的交互作用

如
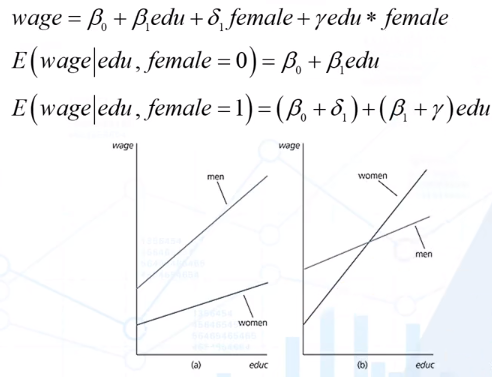
\begin{align} & y=\beta_0+\delta_1d+\beta_1x+\delta_2dx+u\\ & E(y|x,d=0)=\beta_0+\beta_1x\\ & E(y|x,d=1)=(\beta_0+\delta_1)+(\beta_1+\delta_2)x \end{align}
用一个回归方程允许了两种不同的截矩与斜率

样条回归

使得X对Y的边际影响在X自己的特定取值范围内分段
\begin{align} & income=\beta_0+\beta_1age+\gamma_1d_1+\gamma_2d_2+\delta_1d_1age+\delta_2d_2adge+u\\ & d_1=1\quad if\quad 18\le age\lt 22\\ & d_2=1\quad if\quad age\ge 22\\ & \begin{align} \therefore E(income|age) & =\beta_0+\beta_1age\quad if\ age\lt18\\ & =\beta_0+\gamma_1+(\beta_1+\delta_1)age\quad if\ 18\le age\lt22\\ & =\beta_0+\gamma_1+\gamma_2+(\beta_1+\delta_1+\delta_2)age\quad if\ age\ge 22\\ \end{align} \end{align}

邹氏检验

对于y=\beta_0+\delta_1d+\beta_1x+\delta_2dx+u
H_0:\delta_1=0,\delta_2=0\quad vs.\quad H_1:\delta_1,\delta_2不全为0
假设两组数据的方程有结构差异，分别用第一组数据估计模型得到残差平方和SSR_1，用第二组数据估计模型得到残差平方和SSR_2，两者之和是无约束模型的残差平方和；
如果两组数据的方程没有结构差异，则使用全部数据估计模型得到残差平方和SSR，这是约束模型的残差平方和；
F=\frac{SSR-(SSR_1+SSR_2)}{SSR_1+SSR_2}\frac{n-2(k+1)}{k+1}\sim F(n-2(k+1),k+1)

双重差分

• 如果其他的控制变量可观测且可获得，可以使用多元回归来控制其他变量的影响；
  如果其他变量不可观测，但对因变量的影响不随时间改变，我们可以考虑使用两期的数据，其中第一期是在处理效应发生之前：
• 一般形式
  \begin{align} & y_t=\beta_1+\beta_2T_t+\beta_3D+\beta_4T_t\times D+u_t\quad t=1,2\\ & (y_1|D=1)-(y_2|D=1)=\beta_2+\beta_4\\ & (y_1|D=0)-(y_2|D=0)=\beta_2\\ & [(y_1|D=1)-(y_2|D=1)]-[(y_1|D=0)-(y_2|D=0)]=\beta_4 \end{align}
  

二值变量回归

线性概率模型

1. \begin{align} & y=\beta_0+\beta_1x+u \\ & P(y=1|x)=\beta_0+\beta_1x \end{align}
2. 此时R-Squared不是一个特别有用的统计量
3. 线性概率模型一定是异方差的

非线性概率模型

1. Prohit模型
   P(y=1|x)=\phi(\beta_0+\beta_1x)
2. Logit模型
   P(y=1|x)=\frac{1}{1+e^{-(\beta_0+\beta_1x)}}

模型的估计

因为是非线性模型，无法使用OLS，改用极大似然估计（MLE）
在大样本情况下，MLE具有一致性、正态分布性、有效性

1. 单变量的 Probit 似然估计
   \begin{align} & Pr(y_1=1|x_1)=\phi(\beta_0+\beta_1x_1) \\ & Pr(y_1=0|x_1)=1-\phi(\beta_0+\beta_1x_1) \\ & 概率分布函数\quad \phi(\beta_0+\beta_1x_1)^{y_1}[1-\phi(\beta_0+\beta_1x_1)^{1-y_1}] \\ & 联合密度函数\quad f(\beta_0,\beta_1;y_1,\dots,y_n|x_1,\dots,x_n)=\Pi_{i=1}^{n} \phi(\beta_0+\beta_1x_i)^{y_i}[1-\phi(\beta_0+\beta_1x_i)^{1-y_i}] \end{align}
   通过数值方法获取解和标准差
2. 单变量的 Logit 似然估计
   类似Probit

推断及拟和好坏的评价

1. MLE估计量的特性
   是一致估计量
   具有正态分布性
   可以计算它们的标准差
   参数的检验和区间估计同经典的模型一样

2. 拟合度量
   预测正确的概率
   伪R^2

其他受限因变量模型

1. 多元选择模型
   一个人选择上班时所采用的方式——自己开车，乘出租车，乘公共汽车，还是骑自行车。
2. 有序选择模型
   在有序因变量模型中，能被观察到的y指出了代表排序或排列的种类的结果。例如，我们可以察选择处于四种教育结果之一的个体：高中以高中、大学、硕士及更高学位。
   设有一个潜在变量y^\ast，是不可观测的，可观测的是y,有0,1,\dots,M等M+1个取值。
   \begin{align} & y^\ast=\beta x+u \\ & y=\begin{cases} & 0 & \quad if\ y_i^\ast\le c_1\\ & 1 & \quad if\ c_1\lt y_i^\ast\le c_2 \\ & \vdots \\ & M & \quad if\ c_M\lt y_i^\ast \end{cases} \end{align}\\ \begin{align} \therefore & P(y_i=0)=F(c_1-\beta x_i) \\ & P(y_i=1)=F(c_2-\beta x_i)-P(y_i=0)\\ & P(y_i=2)=F(c_3-\beta x_i)-P(y_i=1)\\ & \vdots \\ & P(y_i=M)=1-P(y_i=M-1) \end{align}
   F可以取Prohit和Logit
   c_i也需要估计